Базисные решения

Справочный материал.

Если ранг матрицы системы равен рангу расширенной матрицы системы и равен числу неизвестных: , то система имеет единственное решение. Если ранг матрицы системы равен рангу расширенной матрицы системы и меньше числа неизвестных: , то система имеет бесконечное множество решений.

Если система имеет бесконечное множество решений, то r переменных, определитель матрицы коэффициентов при которых отличен от нуля, объявляют основными переменными; остальные n−r переменных называют свободными. Свободным переменным можно придать любое числовое значение.

Решение системы, в котором все свободные переменные равны нулю, называется базисным решением.

Пример. Найти все базисные решения системы:

Решение. Решим систему методом Гаусса. Запишем расширенную матрицу системы:

.

Приведём расширенную матрицу системы к ступенчатому виду. Для этого выполним следующие преобразования.

1) Прибавим к первой строке вторую, умноженную на 3:

.

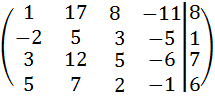2) Прибавим ко второй строке первую, умноженную на 2; прибавим к третьей строке первую, умноженную на (−3); прибавим к четвёртой строке первую, умноженную на (−5):

.

3) Прибавим к третьей строке вторую; прибавим к четвёртой строке вторую, умноженную на 2:

.

4) Вычеркнем нулевые строки:

.

Расширенная матрица приведена к ступенчатому виду. Ранг матрицы системы равен 2, ранг расширенной матрицы системы также равен 2: , то есть система совместна. Так как ранг меньше числа неизвестных: , то система имеет бесконечное множество решений. Две переменные объявляем основными, остальные две – свободными. Возможны следующие пары основных переменных: 1) ; 2) ; 3) ; 4) ; 5) ; 6) . Выясним могут ли эти пары переменных быть основными. Для этого вычислим определитель матрицы из коэффициентов при этих неизвестных. Если определитель отличен от нуля, то указанную пару можно взять в качестве основных переменных. На основе ступенчатой матрицы запишем систему уравнений:

1) Выясним могут ли переменные быть основными. Составляем определитель матрицы из коэффициентов при этих неизвестных: . Так как определитель отличен от нуля, то неизвестные могут быть основными. Остальные переменные объявляем свободными. Приравняем свободные переменные нулю: 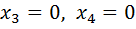, получим следующую систему уравнений: Решение этой системы: , . Таким образом, получаем первое базисное решение: .

2) Выясним могут ли переменные быть основными. Составляем определитель матрицы из коэффициентов при этих неизвестных: . Так как определитель отличен от нуля, то неизвестные могут быть основными. Остальные переменные объявляем свободными. Приравняем свободные переменные нулю: , получим следующую систему уравнений: Решение этой системы: , . Таким образом, получаем второе базисное решение: .

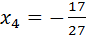3) Выясним могут ли переменные быть основными. Составляем определитель матрицы из коэффициентов при этих неизвестных: . Так как определитель отличен от нуля, то неизвестные могут быть основными. Остальные переменные объявляем свободными. Приравняем свободные переменные нулю: , получим следующую систему уравнений: Решение этой системы: , . Таким образом, получаем третье базисное решение: .

4) Выясним могут ли переменные быть основными. Составляем определитель матрицы из коэффициентов при этих неизвестных: . Так как определитель отличен от нуля, то неизвестные могут быть основными. Остальные переменные объявляем свободными. Приравняем свободные переменные нулю: , получим следующую систему уравнений: Решение этой системы: , . Таким образом, получаем четвёртое базисное решение: .

5) Выясним могут ли переменные быть основными. Составляем определитель матрицы из коэффициентов при этих неизвестных: . Так как определитель отличен от нуля, то неизвестные могут быть основными. Остальные переменные объявляем свободными. Приравняем свободные переменные нулю: , получим следующую систему уравнений: Решение этой системы: , . Таким образом, получаем пятое базисное решение: .

6) Выясним могут ли переменные быть основными. Составляем определитель матрицы из коэффициентов при этих неизвестных: . Так как определитель отличен от нуля, то неизвестные могут быть основными. Остальные переменные объявляем свободными. Приравняем свободные переменные нулю: , получим следующую систему уравнений: Решение этой системы: , . Таким образом, получаем шестое базисное решение: .

Ответ: , , , , , .

Задание 23. Найти все базисные решения системы уравнений.

1.

2.

3.

4.

5.

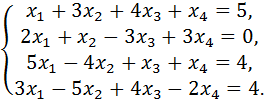
6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

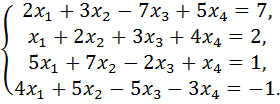
18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

33.

34.

35.

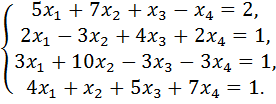
36.