 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Знакоопределённость квадратичной формы
|
|
Нормальным видом квадратичной формы называют сумму квадратов нескольких неизвестных с коэффициентами +1 или –1.
Квадратичная форма L от n неизвестных с действительными коэффициентами называется положительно определённой, если она приводится к нормальному виду, состоящему из n положительных квадратов.
Квадратичная форма L от n неизвестных с действительными коэффициентами называется отрицательно определённой, если она приводится к нормальному виду, состоящему из n отрицательных квадратов.
Квадратичная форма 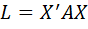 положительно определена тогда и только тогда, когда: все собственные значения матрицы
положительно определена тогда и только тогда, когда: все собственные значения матрицы  положительны или все главные миноры матрицы
положительны или все главные миноры матрицы  положительны (Критерий Сильвестра).
положительны (Критерий Сильвестра).
Квадратичная форма 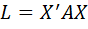 отрицательно определена тогда и только тогда, когда: все собственные значения матрицы
отрицательно определена тогда и только тогда, когда: все собственные значения матрицы  отрицательны или все главные миноры матрицы
отрицательны или все главные миноры матрицы  нечётного порядка отрицательны, а чётного порядка положительны (Критерий Сильвестра).
нечётного порядка отрицательны, а чётного порядка положительны (Критерий Сильвестра).
Пример. Исследовать квадратичную форму 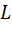 на знакоопределённость:
на знакоопределённость:
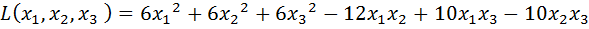 .
.
Решение.
Первый способ. (С помощью собственных значений.)
Запишем матрицу квадратичной формы:
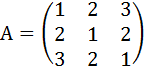 .
.
Найдём собственные значения матрицы  . Для этого составим характеристическое уравнение:
. Для этого составим характеристическое уравнение:
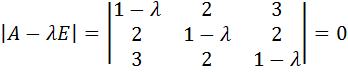 .
.
Выполним преобразования, не меняющие значение определителя. Прибавим к третьей строке первую, умноженную на (–1):
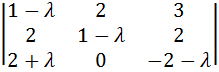 .
.
Прибавим к третьему столбцу первый:
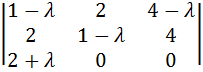 .
.
Раскроем определитель разложением по третьей строке:
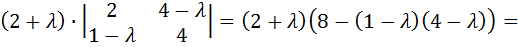
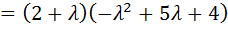 .
.
Уравнение 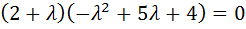 имеет следующие корни:
имеет следующие корни: 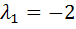 ,
, 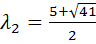 ,
, 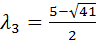 .
.
Так как среди собственных значений матрицы  есть положительные и отрицательные, то квадратичная форма не является знакоопределённой.
есть положительные и отрицательные, то квадратичная форма не является знакоопределённой.
Второй способ. (С помощью критерия Сильвестра.) Вычислим главные миноры матрицы  :
:
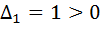 ,
, 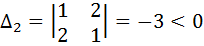 .
.
Так как критерий Сильвестра не выполняется, то квадратичная форма не является знакоопределённой.
Ответ: квадратичная форма не является знакоопределённой.
Задание 22. Исследовать квадратичную форму L на знакоопределённость.
1. 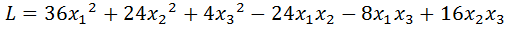 .
.
2. 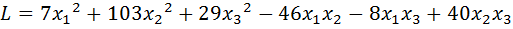 .
.
3. 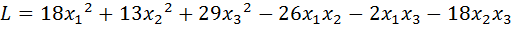 .
.
4. 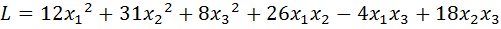 .
.
5. 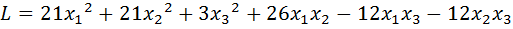 .
.
6. 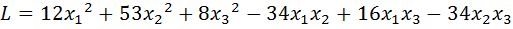 .
.
7. 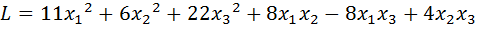 .
.
8. 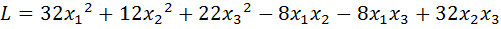 .
.
9. 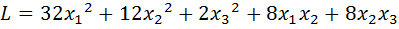 .
.
10. 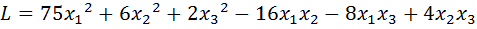 .
.
11. 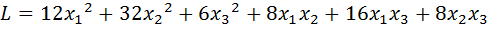 .
.
12. 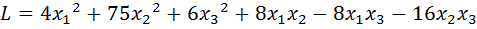 .
.
13. 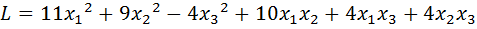 .
.
14. 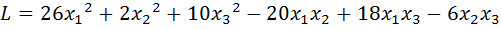 .
.
15. 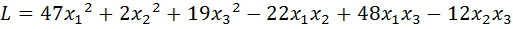 .
.
16. 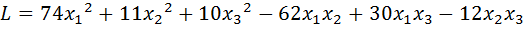 .
.
17. 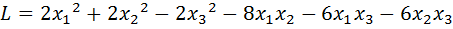 .
.
18. 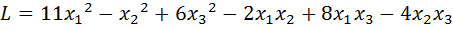 .
.
19. 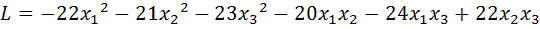 .
.
20. 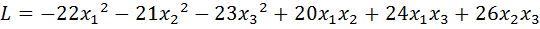 .
.
21. 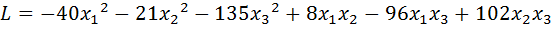 .
.
22. 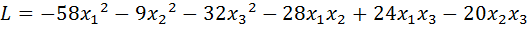 .
.
23. 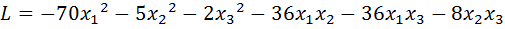 .
.
24. 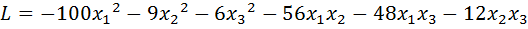 .
.
25. 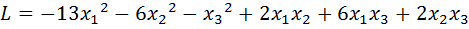 .
.
26. 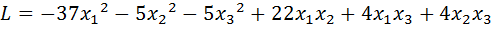 .
.
27. 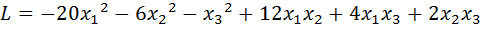 .
.
28. 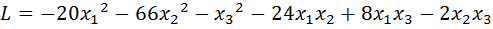 .
.
29. 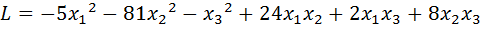 .
.
30. 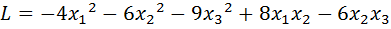 .
.
31. 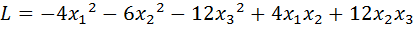 .
.
32. 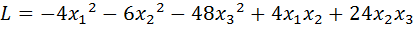 .
.
33. 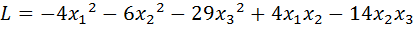 .
.
34. 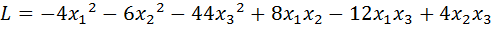 .
.
35. 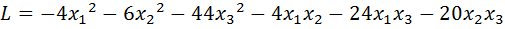 .
.
36. 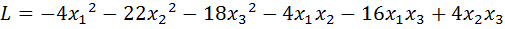 .
.
Дата публикования: 2015-10-09; Прочитано: 2507 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
