 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Обратная матрица. Если – квадратная матрица, то обратной для неё называется матрица, обозначаемая и удовлетворяющая условиям
|
|
Справочный материал.
Если  – квадратная матрица, то обратной для неё называется матрица, обозначаемая
– квадратная матрица, то обратной для неё называется матрица, обозначаемая 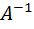 и удовлетворяющая условиям
и удовлетворяющая условиям 
 , где Е – единичная матрица.
, где Е – единичная матрица.
Теорема. Обратная матрица существует тогда и только тогда, когда исходная матрица  невырожденная (определитель матрицы
невырожденная (определитель матрицы  не равен нулю).
не равен нулю).
Обратную матрицу можно найти двумя способами.
Первый способ (с помощью присоединённой матрицы).
 , где
, где  – присоединённая матрица (получена транспонированием матрицы, составленной из алгебраических дополнений
– присоединённая матрица (получена транспонированием матрицы, составленной из алгебраических дополнений  элементов
элементов 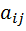 матрицы
матрицы  ).
).
Можно записать:
 .
.
Второй способ (с помощью элементарных преобразований). К матрице  размерности
размерности  приписывают справа единичную матрицу размерности
приписывают справа единичную матрицу размерности  . Получают прямоугольную матрицу
. Получают прямоугольную матрицу  размерности
размерности  . С помощью элементарных преобразований над строками матрицу
. С помощью элементарных преобразований над строками матрицу 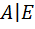 приводят к ступенчатому виду
приводят к ступенчатому виду  , где
, где 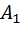 – треугольная матрица; затем матрицу
– треугольная матрица; затем матрицу  приводят к виду
приводят к виду 
Пример. Дана матрица  . Найти для неё обратную
. Найти для неё обратную 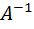 .
.
Решение.
Первый способ.
Вычислим определитель матрицы  :
:  . Так как
. Так как 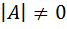 , то матрица
, то матрица  – невырожденная и для неё существует обратная.
– невырожденная и для неё существует обратная.
Найдём алгебраические дополнения всех элементов матрицы  .
.
 ;
;

 ;
;

 ;
;
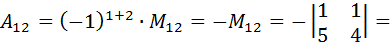
 ;
;
 ;
;
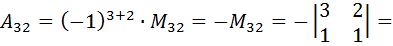
 ;
;

 ;
;

 ;
;

Составим обратную матрицу:

 .
.
Второй способ. Запишем матрицу 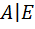 :
:
 .
.
С помощью элементарных преобразований приведём матрицу 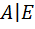 к ступенчатому виду.
к ступенчатому виду.
1. Поменяем местами первую и вторую строки:
 .
.
2. Ко второй строке прибавим первую, умноженную на (–3), к третьей строке прибавим первую, умноженную на (–5):
 .
.
3. Вторую строку умножим на 12, третью строку умножим на (–7):
 .
.
4. К третьей строке прибавим вторую:
 .
.
5. Вторую строку разделим на (–12):
 .
.
Последнюю матрицу приведём к виду  .
.
6. Разделим вторую строку на 7, третью строку разделим на (–5):
 .
.
7. Ко второй строке прибавим третью, умноженную на 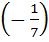 :
:
 .
.
8. Прибавим к первой строке вторую, умноженную на (–3):
 .
.
9. Прибавим к первой строке третью, умноженную на (–1):
 .
.
Таким образом,  .
.
Сделаем проверку. Для этого умножим обратную матрицу 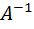 на данную матрицу
на данную матрицу  , используя операции умножения матриц и умножения матрицы на число:
, используя операции умножения матриц и умножения матрицы на число:

 .
.
Так как в результате получилась единичная матрица, то обратная матрица найдена правильно.
Ответ:  .
.
Задание 8. Дана матрица  . Найти для неё обратную
. Найти для неё обратную 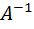 .
.
1.  . 2.
. 2.  .
.
3.  . 4.
. 4.  .
.
5.  . 6.
. 6.  .
.
7.  8.
8.  .
.
9.  . 10.
. 10. 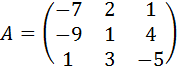 .
.
11.  . 12.
. 12.  .
.
13. 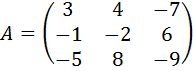 . 14.
. 14.  .
.
15.  . 16.
. 16.  .
.
17.  . 18.
. 18.  .
.
19.  . 20.
. 20.  .
.
21.  . 22.
. 22.  .
.
23.  . 24.
. 24.  .
.
25. 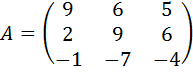 . 26.
. 26.  .
.
27.  . 28.
. 28.  .
.
29.  . 30.
. 30.  .
.
31.  . 32.
. 32.  .
.
33.  . 34.
. 34.  .
.
35.  . 36.
. 36.  .
.
Дата публикования: 2015-10-09; Прочитано: 482 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
