 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Уравнений
|
|
Справочный материал.
1. Правило Крамера. По правилу Крамера можно решать системы, когда число уравнений равно числу неизвестных.
Теорема. Пусть 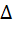 − определитель матрицы системы, а
− определитель матрицы системы, а 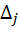 − определитель, полученный из
− определитель, полученный из 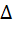 заменой j -ого столбца столбцом свободных элементов. Тогда если
заменой j -ого столбца столбцом свободных элементов. Тогда если  , то система уравнений имеет единственное решение, определяемое по формулам
, то система уравнений имеет единственное решение, определяемое по формулам 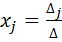 ,
,  .
.
2. Метод обратной матрицы. Методом обратной матрицы можно решать системы, когда число уравнений равно числу неизвестных Если матрица системы невырожденная, то матрицу неизвестных находят по формуле  .
.
3. Метод Гаусса. Методом Гаусса можно решать системы с любым числом уравнений и неизвестных. Этот метод основан на приведении расширенной матрицы системы с помощью элементарных преобразований (приводящих к эквивалентной системе) к ступенчатому виду с последующим постепенным нахождением неизвестных, начиная с последних неизвестных.
Пример. Решить систему линейных алгебраических уравнений по правилу Крамера, методом обратной матрицы и методом Гаусса:

Решение.
1. Правило Крамера.
Так как число уравнений равно числу неизвестных и определитель матрицы системы (определитель, составленный из коэффициентов при неизвестных) отличен от нуля:


 ,
,
то правило Крамера применимо.
Вычислим определитель  , который получается из
, который получается из 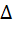 заменой первого столбца столбцом свободных элементов:
заменой первого столбца столбцом свободных элементов:


 .
.
Вычислим определитель 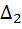 , который получается из
, который получается из 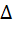 заменой второго столбца столбцом свободных элементов:
заменой второго столбца столбцом свободных элементов:


 .
.
Вычислим определитель  , который получается из
, который получается из 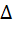 заменой третьего столбца столбцом свободных элементов:
заменой третьего столбца столбцом свободных элементов:


 .
.
Тогда  ,
,  ,
, 
 .
.
Ответ:  .
.
2. Метод обратной матрицы.
Составим матрицу системы  , матрицу неизвестных
, матрицу неизвестных 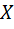 и матрицу свободных элементов
и матрицу свободных элементов 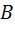 :
:
 ,
,  ,
,  .
.
Так как число уравнений равно числу неизвестных и определитель матрицы системы  , то метод обратной матрицы применим.
, то метод обратной матрицы применим.
Используем формулу  .
.
Найдём обратную матрицу  , где
, где  − определитель матрицы системы,
− определитель матрицы системы,  – алгебраические дополнения элементов матрицы
– алгебраические дополнения элементов матрицы  .
.
Вычислим алгебраические дополнения элементов матрицы  :
:
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
 ;
;
Составим обратную матрицу:
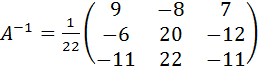 .
.
Найдём матрицу неизвестных X:

 .
.
Ответ:  .
.
3. Метод Гаусса.
Запишем расширенную матрицу системы и приведём её к ступенчатому виду с помощью элементарных преобразований, приводящих к эквивалентной системе.
 .
.
Выполним следующие преобразования.
1) Ко второй строке прибавим первую, умноженную на (−1):
 .
.
2) Поменяем первую и вторую строки местами:
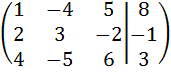 .
.
3) Прибавим ко второй строке первую, умноженную на −2; к третьей строке прибавим первую, умноженную на −4:
 .
.
4) Прибавим к третьей строке вторую, умноженную на (−1):
 .
.
На основе последней матрицы запишем систему уравнений:

Из последнего уравнения находим  . Подставляя
. Подставляя  во второе уравнение, находим
во второе уравнение, находим  . И подставляя
. И подставляя  ,
,  в первое уравнение, находим
в первое уравнение, находим  .
.
Ответ:  .
.
Задание 9. Решить систему линейных алгебраических уравнений по правилу Крамера, методом обратной матрицы и методом Гаусса.
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 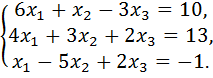
9.  10.
10. 
11.  12.
12. 
13.  14.
14. 
15. 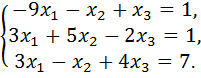 16.
16. 
17.  18.
18. 
19.  20.
20. 
21.  22.
22. 
23.  24.
24. 
25.  26.
26. 
27.  28.
28. 
29.  30.
30. 
31.  32.
32. 
33.  34.
34. 
35.  36.
36. 
Дата публикования: 2015-10-09; Прочитано: 336 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
