Дәріс №3. Бір белгісізі бар теңдеулерді шешудің Хорда әдісі және жанама әдісі

Жоспар:

1. Бір белгісізі бар теңдеулерді шешудің кесіндіні хорда және жанама әдістері, олардың геометриялық мағынасы.

2. Хорда және жанама әдістерін қолдана отырып берілген есептердің бағдарламасын құру және оны ЭЕМ-де жүзеге асыру.

3. Қателіктерін бағалау.

Кілттік сөздер: Х орда, жанама, формула, қателік

1. Бізге F(x)=0 теңдеуі берілсін. Осы F(x)-функциясының x-осімен қиылысқан жерлеріндегі түбірін табу керек, біздің графигімізде ол түбір А-арқылы көрсетілген.

3-сурет. Хорда әдісінің геометриялық кескіндеме түріндегі көрінісі.

Оны табу үшін функцияның шеткі нүктелері ММ* нүктелерін қосатын Хорда жүргіземіз. Осы хорданың х осімен қилысқан нүктесін D₁ деп белгілейміз де осы нүктеден Хорданы қосатындай у осіне параллель түзу жүргіземіз. Оны M₁ деп белгілейміз. Енді [M₀, M*]- нүктелерінен өтетін түзудің теңдеуін жазамыз.

Формуламен сәйкестендіру сіздерге тапсырма ретінде беріледі. Жалпы түрде бір белгісізі бар теңдеулерді хорда әдісімен шешудің жолы 3-суретте келтірілді.

мұндағы бұдан 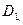- ді табамыз. Сонда

Енді ]- нүктелерінен өтетін Хорданың теңдеуін жазамыз.

деп белгілеп алып, 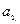-ні табамыз да осы процесті жалғастыра береміз.

Енді тізбегінің шегін табамыз.

бұл Хорда әдісінің жалпы формуласы болып табылады. Бірақ, мұнда есептелінген -нің мәнінің дәлдігін қалайша бағалау мәселесі шешілмей отыр.

Бұл мәселені шешу үшін айырмасына шектеулі өсімшелер формуласын қолданамыз:

Мұнан

егер де қарастырылып отырған аралықта (оны алдын ала біржолата есептеп қоюға болады) -тің ең кіші мәнін m - мен белгілесек, онда былайша бағалауға болады:

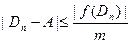
Сөйтіп, шамасы бойынша да -нің түбірге қаншалықты жақындығын айтуға болады екен.