Теорема. Плоская система произвольно расположенных сил в общем случае эквивалентна одной силе, приложенной в центре приведения О

Плоская система произвольно расположенных сил в общем случае эквивалентна одной силе, приложенной в центре приведения О, и одной паре.

Рисунок 44

Доказательство

Пусть дана плоская система (рисунок 44-а) трех сил (F₁, F₂, F₃). Перенесем параллельно все силы в центр приведения О (), добавив при этом три пары сил с моментами:

М₁ = М₀ (F ₁) = F₁· l ₁;

М₂ = М₀ (F ₂) = F₂· l ₂;

М₃ = М₀ (F ₃) = F₃· l ₃.

Найдем равнодействующую сходящихся сил (), сложив их по правилу силового многоугольника (рисунок 44-б):

.

Вектор равнодействующей, равный геометрической сумме векторов всех сил, называется главным вектором F_гл:

(13)

Все три присоединенные пары, лежащие в одной плоскости, можно сложить, получив одну пару, момент которой равен алгебраической сумме моментов присоединенных пар. Этот момент называется главным моментом М_гл:

:

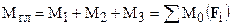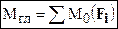(14)

Таким образом, произвольная плоская система сил эквивалентна одной силе F_гл и одной паре с моментом М_гл.

Теорема доказана.