Загальні положення. Інтерполяційний многочлен Лагранжа в загальному випадку має вигляд: , де – коефіцієнт полінома Лагранжа

Інтерполяційний многочлен Лагранжа в загальному випадку має вигляд: 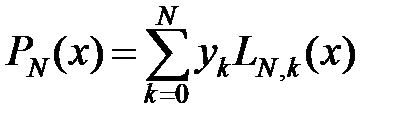, де 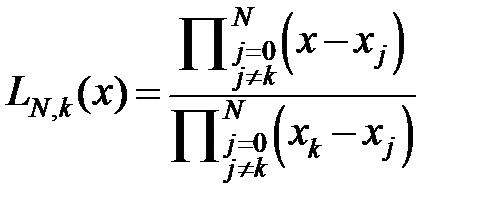– коефіцієнт полінома Лагранжа. При цьому його залишковий член матиме наступний вигляд: 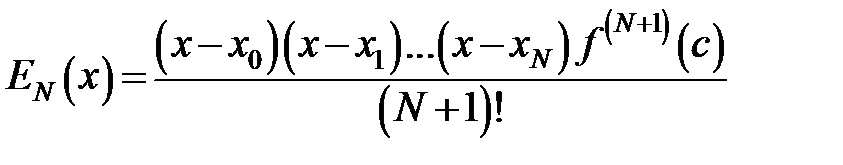, де .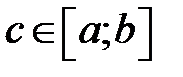

Інтерполяційний многочлен Ньютона в загальному випадку виглядає наступним чином: 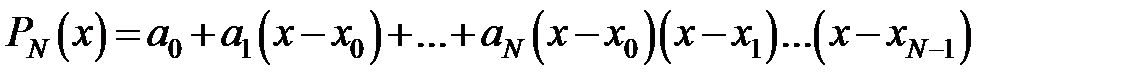, де 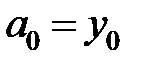, a коефіцієнти 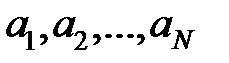є різничним відношенням функції 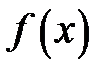. Тому для їх знаходження можна використати формулу для різничних відношень 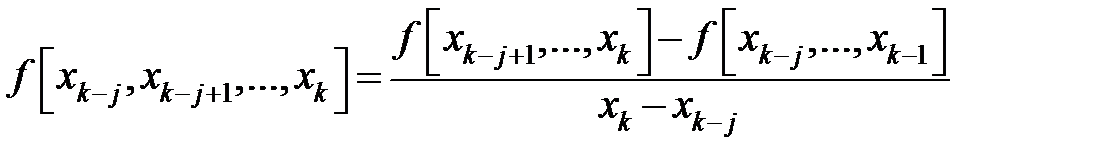. В даному випадку залишковий член матиме такий же вигляд, як і в попередньому.

Формула розподілу Чебишевських вузлів на проміжку :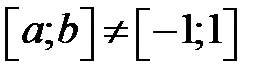

.

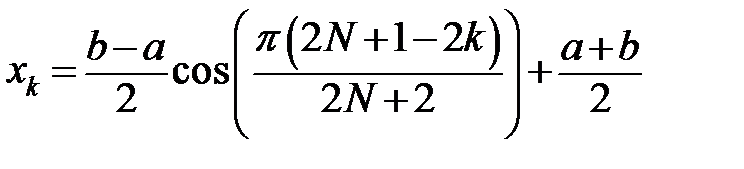Кусково-лінійна інтерполяція являє собою так звану інтерполяцію лінійними сплайнами. В загальному вигляді формула для даного методу

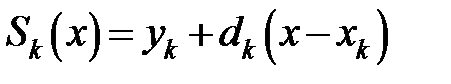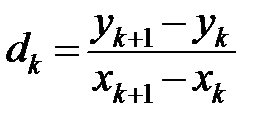матиме наступний вигляд: , де , при 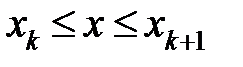. Її також можна переписати наступним чином:

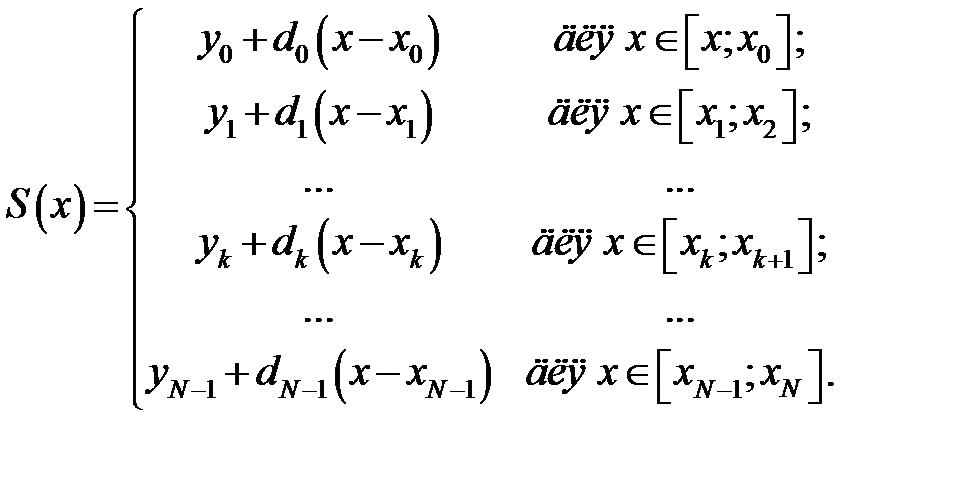
Функція 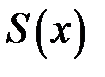називається кубічним сплайном, якщо існує 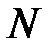кубічних поліномів 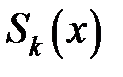з коефіцієнтами 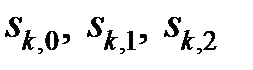та 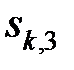, які задовольняють наступним умовам:

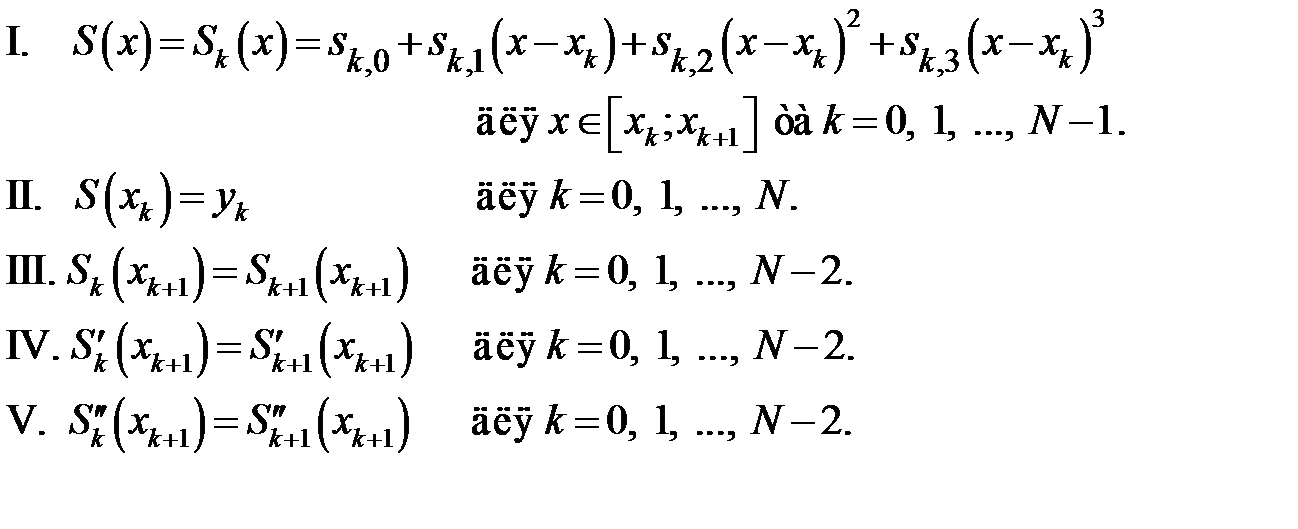
Де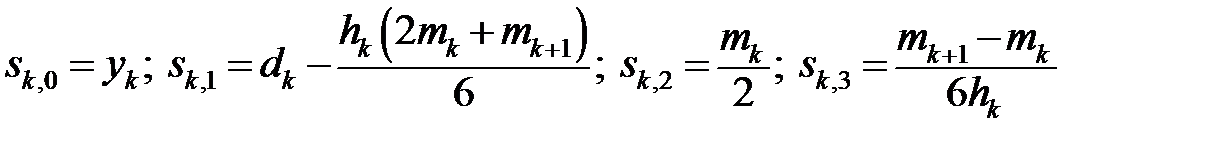

Таблиця 6.1 - Обмеження в граничних точках для кубічного сплайна

Опис стратегії Рівняння відносно m₀і m_N