Mетод Эйлера

Простой метод Эйлера реализуется применением на каждом шаге вычислений следующих итерационных выражений:

x_i+1=x₁+h;

y_i+1=y₁+h*f(x,y). (27)

При этом для i = 0 значения x₀ и y₀ должны быть известны как начальные условия. Погрешность метода пропорциональна h².

Для уменьшения погрешности решения следует применять более точные методы. Например, метод Эйлера с пересчетом реализуется следующими итерационными выражениями на каждом шаге вычислений:

x_i+1=x₁+h;

y_i+1=y₁+h*(f(x₁,y₁)+f(x₁+h,y₁+h*f(x₁,y₁)))/2 (28)

Погрешность метода пропорциональна h³.

Метод Рунге-Кутта

При высоких требованиях к точности решения можно воспользоваться методом Рунге-Кутта, реализующийся следующими формулами:

k1 = h* f(x_i,y_i);

k2 = h* f(x_i+h/2,y_i+k1/2);

k3 = h* f(x_i+h/2,y_i+k2/2); (29)

k4=h*f(x_i+h,y_i+k3);

x_i+1 = x_i + h;

y_i+1 = y_i + (k1+2*k2+2*k3+k4)/6.

Погрешность метода пропорциональна h⁵.

Для решения обыкновенных дифференциальных уравнений 2-го порядка Y''+p(x)Y'+g(x)Y=f(x) с граничными условиями:

k11*Y(a)+k12*Y' (a)=A,

k21*Y(b)+k22*Y´(b)=B

также применяется метод конечных разностей, при этом производные, входящие в уравнение и дополнительные условия заменяются следующими конечно-разностными отношениями:

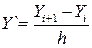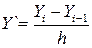; ; ; (30)

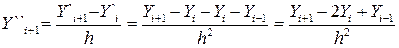. (31)

В результате получим систему алгебраических уравнений, решение которой даст таблицу приближенных значений искомой функции.

ПРИМЕР. Решить обыкновенное дифференциальное уравнение 2-го порядка:

y''+xy'-0.5y/x=1

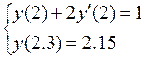
Решение:

Разбив отрезок [2, 2.3] на части с шагом h = 0.1, получим четыре узловые точки с абсциссами x₀ =2, x₁ =2.1, x₂ =2.2, x₃ =2.3. Две точки x₀ =2 и x₃ =2.3 являются конечными, две другие – внутренними. Данное уравнение во внутренних точках заменим конечно-разностным:

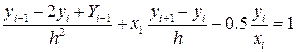(i= 1, 2).

Из краевых условий составим конечно-разностные уравнения в конечных точках:

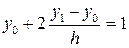, y3=2.15.

Задача сводится к решению системы уравнений:

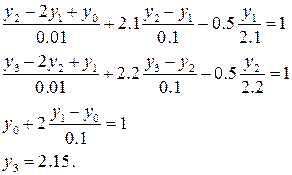
Примеры решения дифференциальных уравнений с помощью встроенных функций системы MathСad приведены в приложениях Д, Е.

Задание 4.2. Решите на отрезке [ x₀,x_end ] задачу Коши методом Рунге-Кутта с постоянным шагом. Вид уравнения и начальные значения заданы в таблице 3. Изобразите графики решений, вычисленных с шагами h, 2 h и h /2.

Таблица 3 – Данные для расчета

Вариант	Функция	x0	xend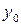
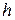
					0.1
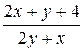
					0.1
					0.1
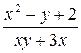
					0.1
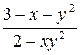
					0.1
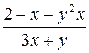
					0.1
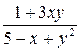
					0.1
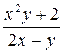
					0.1
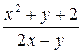
					0.1
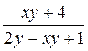
					0.1
					0.1
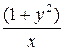
					0.1

Порядок выполнения задания:

1. Присвойте начальное значение решения переменной у₀.

2. Определите правую часть уравнения f(x,y).

3. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= .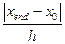

4. Сохраните решение в матрице У1.

5. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= 2 .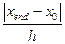

6. Сохраните решение в матрице У2.

7. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= .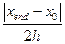

8. Сохраните решение в матрице У3.

9. Постройте на одном графике все три найденных решения.

10. Оцените погрешности найденных решений по формуле Рунге.

Задание 4.3. Решите задачу Коши

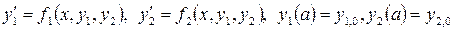на отрезке [ a,b ] методом Рунге-Кутты с постоянным шагом h =0.1. Изобразите графики решений, вычисленных с шагом h, 2 h и h /2. Вид уравнений и начальные значения заданы в таблице 4.

Таблица 4 – Данные для расчета

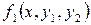
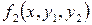
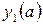
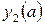
Вариант					a	b
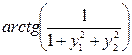
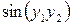
					-1
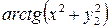
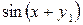
			0.5	1.5
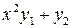
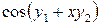
			-1

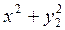
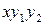
Продолжение таблицы 4

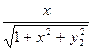
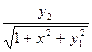
			0.2		-1
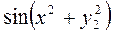
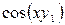
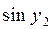
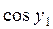
			0.5	-0.5	-1
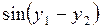
			-0.6
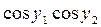
					-1
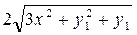
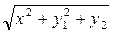
			1.2	1.2
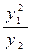
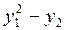
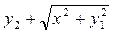
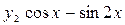
			0.8	3.5

Порядок выполнения задания:

1. Присвойте переменной ORIGIN значение, равное единице.

2. Присвойте начальное значение решения переменной у₀.

3. Определите правую часть уравнения f(x,y).

4. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= .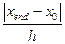

5. Сохраните решение в матрице У1.

6. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= 2 .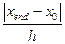

7. Сохраните решение в матрице У2.

8. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= .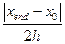

9. Сохраните решение в матрице У3.

10. Постройте на одном графике все три найденные решения.

11. Оцените погрешности найденных решений по формуле Рунге.

Задание 4.4. Найдите общее решение линейного однородного уравнения второго порядка 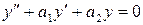. Решите задачу Коши 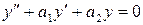, 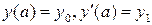. Изобразите его график. Значения параметров а₁, а₂ и а заданы в таблице 5.

Таблица 5 – Данные для расчета

Вариант	a1	a2	y(a)	y¢(a)	a
	-4
					p/2
					-p/2
	-4				0.3
			-1		0.25
					p/2
					-p/2
	-4
	-4		-1	0.5

Порядок выполнения задания:

1. Присвойте переменной ORIGIN значение, равное единице.

2. Присвойте начальное значение решения переменной у₀.

3. Определите правую часть уравнения f(x,y).

4. Вычислите решение, используя функцию rkfixed с параметром N, вычисленным по формуле N= .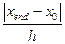

5. Сохраните решение в матрице У1.

Задание 4.5. Постройте графики решения и фазовые портреты динамической системы

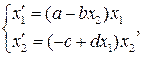
моделирующей взаимодействие популяций при заданных значениях параметров a,b,c,d. Значения параметров заданы в таблице 6. Исследуйте поведение решения, изменяя параметры.

Таблица 6 – Данные для расчета

Вариант	a	b	c	d
		3.5
		3.5
		3.5
		3.5
		3.5
		4.5

Порядок выполнения задания:

1. Присвойте переменной ORIGIN значение, равное единице.

2. Определите вектор-столбец начальных условий для первой задачи Коши.

3. Определите вектор-столбец правых частей системы.

4. Выберите значение шага интегрирования h и вычислите количество шагов N интегрирования системы на отрезке [ x₀,x_end ] по формуле N= .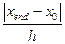

5. Решите задачу Коши для первого начального условия.

6. Изобразите соответствующую фазовую кривую и график решения.

7. Определите векторы-столбцы начальных условий для каждого начального условия.

8. Решите соответствующие задачи, сохранив каждое решение в отдельной матрице.

9. Изобразите соответствующие фазовые кривые и графики решений.

Задание 5.5. Исследуйте поведение системы

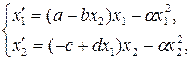
моделирующей взаимодействие популяций. Выполните вычисления для значений a,b,c,d из задания 7.4 для приведённых ниже значений a (таблица 7).

Таблица 7 – Данные для расчета

Вариант	a	Вариант	a	Вариант	a
	0.1		0.05		0.17
	0.15		0.22		0.18
	0.20		0.12		0.1
	0.25		0.14		0.2

Список Литературы

1. Кудрявцев, Е.М. MathCad 8 / Е.М. Кудрявцев - М: ДМК, 2000. - 320с.

2. Плис, А.И. MathCad 2000: математический практикум для экономистов и инженеров: Учебное пособие / А.И. Плис, Н.А. Сли-вина - М.: Финансы и статистика, 2000. - 656с.

3. Турчак, Л.И. Основы численных методов: Учеб. пособие / Л.И. Тучак - М.: Физматлит., 2003. -304с.

4. Информатика: Учеб. пособие / А.В. Могилев, Н.И. Пак, Е.К. Хеннер; Под ред. Е.К. Хеннера. - М.: Издат. центр «Академия», 2004. - 848с.

5. Шуп, Т. Решение инженерных задач на ЭВМ / Т. Шуп - М.: Мир, 1982. -240с.