Формула Симпсона

Формула Симпсона для многочленов 2 степени имеет вид:

(17)

Формула остаточного члена:

;

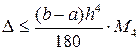(18)

Задание 4.1. Вычислить значение определенного интеграла, заданного в таблице 2.

Таблица 2 – Задания для расчетов

Вариант	Формула интеграла	Вариант	Формула интеграла
	1)			1)
2)		2)
	1)			1)
2)		2)
	1)		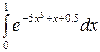	1)
	2)			2)
	1)			1)
2)		2)
	1)			1)
2)		2)
	1)			1)
2)		2)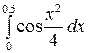

Численное решение обыкновенных дифференциальных уравнений

Дифференциальные уравнения и их системы можно решать численными методами (в частности, методом конечных разностей).

Решение заключается в нахождении ряда значений x_i и y _i искомой зависимости y(x) при i, изменяющемся от 0 до N при шаге изменения х, равном h. Будем рассматривать способы решения дифференциального уравнения, при которых h = const.

Рассмотрим методы решения обыкновенных дифференциальных уравнений первого порядка вида Y' = f(X,Y).