Приемы анализа содержания задачи

Решение текстовой задачи арифметическим способом — это сложная деятельность, содержание которой зависит как от конк­ретной задачи, так и от умений решающего. Тем не менее в ней можно выделить несколько этапов:

1. Восприятие и анализ содержания задачи.

2. Поиск и составление плана решения задачи.

3. Выполнение плана решения. Формулировка вывода о вы­полнении требования задачи (ответа на вопрос задачи).

4. Проверка решения и устранение ошибок, если они есть. Формулировка окончательного вывода о выполнении требова­ния задачи или ответа на вопрос задачи.

Следует подчеркнуть, что в реальном процессе решения задачи отмеченные этапы не имеют четких границ и не всегда выпол­няются одинаково полно. Так, иногда уже при восприятии задачи решающий может обнаружить, что данная задача — известного ему вида и он знает, как ее решать. В этом случае поиск реше­ния не вычленяется в отдельный этап и обоснование, каждого шага при выполнении первых трех этапов делает необязатель­ной проверку после выполнения решения. Однако полное, логи­чески завершенное решение обязательно содержит все этапы. А знание возможных приемов выполнения каждого из этапов делает процесс решения любой задачи осознанным и целенаправ­ленным, а значит, и более успешным.

Основная цель первого этапа решения — понимание ре­шающим в целом ситуации, описанной в задаче, понимание условия задачи, ее требования или вопроса, смысла всех терминов и знаков, имеющихся в тексте.

Известно несколько приемов, применение которых способст­вует пониманию содержания задачи.

Прочитайте, например, такую задачу:

По дороге в одном и том же направлении идут два мальчи­ка. Вначале расстояние между ними было 2 км, но так как ско­рость идущего впереди мальчика 4 км/ч, а скорость второго 5 км/ч, то второй нагоняет первого. С начала движения до то­го, как второй мальчик догонит первого, между ними бегает со­бака со средней скоростью 8 км/ч. От идущего позади мальчика она бежит к идущему впереди, добежав, возвращается обратно и так бегает до тех пор, пока мальчики не окажутся рядом. Какое расстояние пробежит за все это время собака?

Разобраться в содержании этой задачи, вычленить условие и требование ее можно, если задать специальные вопросы по тексту и ответить на них.

1. О чем эта задача? (Задача о движении двух мальчиков и собаки. Это движение характеризуется для каждого его участника! скоростью, временем и пройденным расстоянием.)

2. Что требуется найти в задаче? (В задаче требуется найти расстояние, которое пробежит собака за все это время.)

3. Что обозначают слова «за все это время»? (В задаче го­ворится, что собака бегает между мальчиками «с начала движе­ния до того, как второй мальчик догонит первого». Поэтому слова' «за все это время» означают «за все то время с начала движе­ния, в течение которого второй мальчик догонит первого».)

4. Что в задаче известно о движении каждого из участии, ков его? (В задаче известно, что: 1) мальчики идут в одном на-1 правлении; 2) до начала движения расстояние между мальчиками было 2 км; 3) скорость первого мальчика, идущего впереди, 4 км/ч; 4) скорость второго мальчика, идущего позади, 5 км/ч; 5) скорость бега собаки 8 км/ч; 6) время движения всех участ­ников одинаково: это время от начала движения, когда расстоя­ние между мальчиками было 2 км, до момента встречи мальчи­ков, т. е. до момента, когда расстояние между ними стало 0 км.)

5. Что в задаче неизвестно? (В задаче неизвестно, в течение какого времени второй мальчик догонит первого, т. е. неизвестно время движения всех его участников. Неизвестно также, с какой скоростью происходит сближение мальчиков. И неизвестно рас­стояние, которое пробежала собака — это требуется узнать в задаче.)

6. Что является искомым: число, значение величины, вид некоторого отношения? (Искомым является значение величины — расстояния, которое пробежала собака за общее для всех участни­ков время движения.)

Большую помощь в осмыслении содержания задачи и созда­нии основы для поиска решения задачи оказывает переформу­лировка - текста задачи — замена данного в нем описания ситуа­ции другим, сохраняющим все отношения, связи и количествен­ные характеристики, но более явно их выражающим. Особенно эффективно использование этого средства в сочетании с разбие­нием текста на смысловые части.

Направления переформулировки могут быть следующие: отбрасывание несущественной, излишней информации; замена описания некоторых понятий соответствующими терминами и, наоборот, замена некоторых терминов описанием смысла соот­ветствующих понятий; переорганизация текста задачи в форму, удобную для поиска решения. Результатом переформулировки должно быть выделение основных ситуаций. Так, заметна, что речь в приведенной выше задаче идет о движении, ее можно переформулировать следующим образом:

«Скорость первого мальчика 4 км/ч, а скорость догоняюще­го его второго мальчика 5 км/ч (первая часть задачи). Рас­стояние, на которое мальчики сблизились, 2 км (вторая часть). Время ходьбы мальчиков — это время, в течение которого второй мальчик догонит первого, т. е. в течение которого второй маль­чик пройдет на 2 км больше, чем первый (третья часть). Скорость fiera собаки 8 км/ч. Время бега собаки равно времени ходьбы мальчиков до встречи. Требуется определить расстояние, которое пробежала собака».

Рассмотрим еще такую задачу: «На двух полках книг было на 5 больше, чем на одной из них. Сколько книг было на другой полке?»

После первого прочтения текста кажется, что с задаче не­достает информации о книгах на другой полке. Но попробуем переформулировать задачу, раскрыв смысл отношения «на 5 книг больше». Получим следующий текст: «На двух полках книг столько же, сколько на первой полке, и еще 5 книг. Сколько книг на другой полке?» Переформулируем текст еще раз, заменив в нем слова «на двух полках» словами «на первой и второй полках вместе»: «На первой и второй полках вместе книг столько, сколько на первой полке, и еще 5. Сколько книг на второй пол­ке?» Возможно и дальнейшее уточнение: «Количество книг на первой и второй полках вместе — это количество книг на первой полке и еще 5 книг. Сколько книг на второй полке?»

Из этого текста уже ясно, что 5 книг — это и есть книги на другой полке. Таким образом, в данном случае переформули­ровка привела не только к пониманию содержания задачи, но и (после выполнения несложных логических рассуждений) позво­лила ответить на вопрос задачи.

Переформулированный текст часто бывает полезно записать схематически. Например, содержание первой задачи после форму­лировки можно записать в виде такой таблицы:

Схематическая запись переформулированного текста может иметь и иной вид. Рассмотрим задачу: «Турист проехал 6 ч на поезде со скоростью 56 км/ч. После этого ему осталось ехать в 4 раза больше того, что он проехал. Сколько всего километров он должен был проехать?»

После переформулировки текст может иметь следующий вид:

2) В ящике 100 кг пшена. После того как из ящика насыпали 2 мешка, в нем осталось 10% всего пшена. Сколько пшена на­сыпали в каждый мешок, если в один из них насыпали в 2 раза меньше, чем в другой?

3. Выясните, какой способ записи переформулированного тек­ста (краткая запись, таблица, схематический чертеж) наиболее эффективен для определения плана решения задачи:

С аэродрома вылетел вертолет со скоростью 210 км/ч. Через 2 ч с этого же аэродрома вылетел самолет, который через 3 ч после своего вылета перегнал вертолет на 840 км. Найдите ско­рость самолета.

Приемы поиска плана решения задачи и его выполнение

Одним из наиболее распространенных приемов поиска плана решения задачи арифметическими способами является разбор задачи по тексту (заданному или переформулированному).

Разбор задачи по тексту задачи проводится в виде цепочки рассуждений, которая может начинаться как от данных задачи, так и от ее вопросов.

При разборе задачи от данных к вопросу нужно выделить в тексте задачи два данных и на основе знания связи между ними (такие знания должны быть получены при выполнении первого этапа решения) определить, какое неизвестное может быть найде­но по этим данным и с помощью какого арифметического дейст­вия. Считая это неизвестное данным, надо вновь выделить два взаимосвязанных данных, определить неизвестное, которое может быть найдено по ним, а также соответствующее арифметическое действие и т. д., пока не будет выяснено действие, выполнение которого приводит к получению искомого.

Проведем такой разбор по тексту задачи, рассмотренной в п. 19: «Турист ехал 6 ч по 56 км/ч. Осталось проехать в 4 раза больше, чем проехал. Требуется узнать весь путь».

Рассуждения ведем от данных к вопросу: «Известно, что ту­рист ехал б ч по 56 км/ч. По этим данным можно узнать рас­стояние, которое проехал турист за 6 ч. Для этого достаточно ско­рость умножить на время. Зная пройденное расстояние и то, что оставшееся расстояние в 4 раза больше, можно найти, чему рав­но оставшееся расстояние. Для этого пройденное расстояние нуж­но умножить на 4 (увеличить в 4 раза). Зная, сколько километ­ров турист проехал и сколько ему осталось ехать, можем найти весь путь, выполнив сложение найденных отрезков пути. Итак, первым действием будем находить расстояние, которое турист проехал на поезде; вторым действием — расстояние, которое ему осталось проехать; третьим — весь путь».

При разборе задачи от вопроса к данным нужно обратить внимание на вопрос задачи и установить (на основе информации, полученной при анализе текста задачи), что достаточно узнать

Рис16.

для ответа на вопрос задачи.

Обратиться к условию и выяс­нить,

есть ли для этого необ­ходимые данные. Если таких данных нет или есть только одно данное, то установить, что нужно знать, чтобы найти недостающее данное (недостающие дан­ные), и т. д. Потом составляется план. Рассуждения при этом про­водятся в обратном порядке.

Проведем такой разбор той же задачи, строя цепочку рассуж­дений от вопроса к данным:

«В задаче требуется узнать весь путь. Мы установили, что весь путь состоит из двух частей. Значит, для выполнения тре­бования задачи достаточно знать, сколько километров турист проехал и сколько километров осталось проехать. И то и другое не­известно. Чтобы найти пройденный путь, достаточно знать время и скорость, с которой ехал турнет. Это в задаче известно. Ум­ножив скорость на время, узнаем пройденный путь. Оставшийся путь можно найти, увеличив пройденный путь в 4 раза (умножив на 4). Итак, вначале можно узнать пройденный путь, затем остав­шийся, после чего сложением найти весь путь».

Поиск решения задачи может проводиться по чертежу и по схема­тической записи, составленным на первом этапе.

Покажем, как можно осуществить поиск решения по чертежу. Рассмотрим задачу: «В бидоне было молоко. Сначала из него отлили половину и еще 5 л, а затем 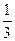оставшегося молока. После этого в бидоне осталось 10 л. Сколько литров молока было в би­доне?»

Пусть отрезок АВ (рис. 16) изображает искомое. По чертежу видно, что этот отрезок разделен на две равные части: АО = ОВ, Отрезок АО состоит из нескольких частей. Причем видно, что от­резок, изображающий 10 л, содержит две из трех равных частей. Тогда один из них будет обозначать (10:2) л, т. е. 5 л. Теперь видно, что эта половина всего отрезка состоит из четырех рав­ных частей, каждая из которых изображает 5 л. Тогда для отве­та на вопрос задачи достаточно умножить 5 на 4 и на 2. Выпол­няя намеченный план, получим 10:2 = 5 (л), 5∙4∙2 = 40 (л).

План решения следующей задачи легко отыскивается после записи текста задачи при помощи таблицы.

Задача. Сколько деталей получится из 36 кг металла, если из 12 кг получается 8 деталей?