 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Плоскость
|
|
Определение 1. Вектор 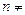 0 называется перпендикулярным плоскости,если он перпендикулярен любому вектору, компланарному этой плоскости. Вектор, перпендикулярный плоскости, называется нормальным вектором (нормалью) этой плоскости.
0 называется перпендикулярным плоскости,если он перпендикулярен любому вектору, компланарному этой плоскости. Вектор, перпендикулярный плоскости, называется нормальным вектором (нормалью) этой плоскости.
Плоскость в пространстве можно задавать различными способами:
1) точкой плоскости и двумя неколлинеарными векторами, компланарными плоскости;
2) тремя точками плоскости, не лежащими на одной прямой;
3) точкой плоскости и ненулевым вектором, перпендикулярным плоскости.
Введем в пространстве СК OXYZ.Уравнение Ax+By+Cz+D 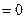 , где
, где 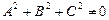 , называется уравнением первого порядка, а поверхность, определяемая этим уравнением – поверхностью первого порядка.
, называется уравнением первого порядка, а поверхность, определяемая этим уравнением – поверхностью первого порядка.
Теорема 1. Поверхности первого порядка есть плоскости и только они.
Уравнение плоскости вида 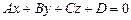 называется общим уравнением плоскости. Нетрудно видеть, что вектор
называется общим уравнением плоскости. Нетрудно видеть, что вектор 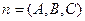 есть нормаль плоскости, заданной уравнением
есть нормаль плоскости, заданной уравнением 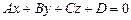 .
.
 Если имеется плоскость
Если имеется плоскость 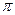 , заданная точкой
, заданная точкой 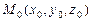 и неколлинеарными векторами
и неколлинеарными векторами 
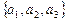 и
и 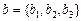 , компланарными этой плоскости, то точка
, компланарными этой плоскости, то точка 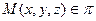 тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 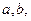 и
и 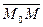 компланарны. Поэтому уравнение плоскости
компланарны. Поэтому уравнение плоскости 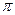 есть
есть

Векторы 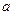 и
и 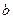 образуют базис на плоскости
образуют базис на плоскости 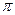 . Разложив вектор
. Разложив вектор 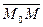 по этому базису, мы получаем параметрические уравнения плоскости
по этому базису, мы получаем параметрические уравнения плоскости 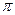 :
:
 , где
, где 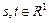 .
.
Если плоскость задана тремя не лежащими на одной прямой точками 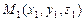 ,
, 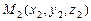 ,
, 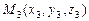 , то, взяв точку
, то, взяв точку  и векторы
и векторы 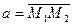 ,
, 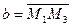 , мы получим уравнение этой плоскости в виде:
, мы получим уравнение этой плоскости в виде:
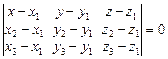 .
.
 Если плоскость
Если плоскость 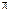 задана вектором
задана вектором 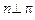 и точкой
и точкой 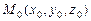 , то точка
, то точка 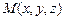
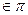 тогда и только тогда, когда вектор
тогда и только тогда, когда вектор 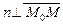 , т.е.
, т.е. 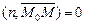 . Поэтому уравнение плоскости
. Поэтому уравнение плоскости 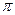 есть
есть 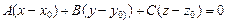 .
.
Исследуем расположение плоскости относительно системы координат.
Теорема 2. Пусть плоскость p задана уравнением 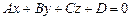 . Тогда:
. Тогда:
1) 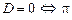 проходит через начало координат.
проходит через начало координат.
2) Если 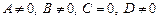 , то
, то 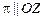 .
.
Аналогично, если 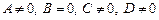 , то
, то 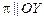 ; если
; если 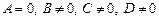 , то
, то 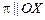 .
.
3) Если 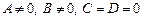 , то
, то 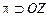 , т.е. плоскость
, т.е. плоскость 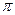 проходит через ось OZ.
проходит через ось OZ.
Аналогично, если 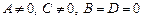 , то
, то 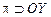 ; если
; если 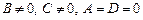 , то
, то  .
.
4) Если 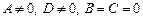 , то
, то 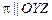 .
.
Аналогично, если  , то
, то 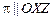 ; если
; если 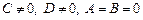 , то
, то 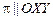 .
.
5) Если 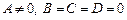 , то
, то 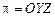 .
.
Аналогично, если 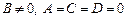 , то
, то 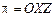 ; если
; если 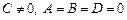 , то
, то 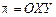 .
.
Пусть заданы две плоскости 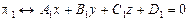 и
и 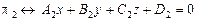 . Возможны три случая взаимного расположения плоскостей
. Возможны три случая взаимного расположения плоскостей  и
и 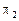 :
:
1)  и
и 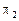 параллельны
параллельны 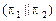 , т.е. не имеют общих точек;
, т.е. не имеют общих точек;
2)  и
и 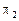 пересекаются, т.е. имеют общие точки, но не совпадают;
пересекаются, т.е. имеют общие точки, но не совпадают;
3) 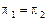 .
.
Теорема 3. 1) 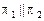 Û
Û 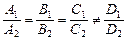 .
.
2)  и
и 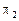 пересекаются Û нарушено одно из равенств в соотношениях
пересекаются Û нарушено одно из равенств в соотношениях 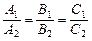 .
.
3) 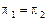 Û
Û 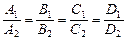 .
.
В случае 2) пересечения плоскостей пересечением плоскостей будет прямая. Эта прямая будет содержать любую точку 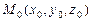 , удовлетворяющую системе
, удовлетворяющую системе 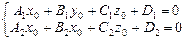 , а за направляющий вектор а этой прямой можно взять векторное произведение нормалей
, а за направляющий вектор а этой прямой можно взять векторное произведение нормалей 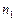 и
и 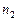 плоскостей, т.е.
плоскостей, т.е. 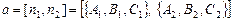 =
= 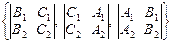 .
.
Как известно, углом между плоскостями  и
и 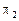 называется любой из двух смежных двугранных углов, образованных этими плоскостями (в случае параллельных плоскостей угол между ними можно считать равным 0 или
называется любой из двух смежных двугранных углов, образованных этими плоскостями (в случае параллельных плоскостей угол между ними можно считать равным 0 или 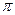 по желанию).
по желанию).  Один из этих углов совпадает с углом между нормалями
Один из этих углов совпадает с углом между нормалями 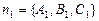 и
и 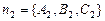 , поэтому справедлива формула
, поэтому справедлива формула 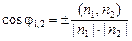 , т.е.
, т.е. 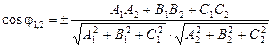 . Условием перпендикулярности плоскостей будет равенство
. Условием перпендикулярности плоскостей будет равенство 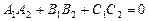 .
.

Расстоянием 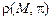 от точки М до плоскости p называется длина перпендикуляра, проведённого из точки М на плоскость p.
от точки М до плоскости p называется длина перпендикуляра, проведённого из точки М на плоскость p.
Теорема 4. Расстояние от точки 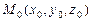 до плоскости p, заданной уравнением
до плоскости p, заданной уравнением 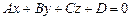 , определяется по формуле
, определяется по формуле
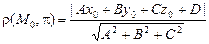 .
.
Две параллельные плоскости  и
и 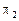 можно задать уравнениями, отличающимися только свободными членами:
можно задать уравнениями, отличающимися только свободными членами: 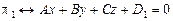 ,
,  . Как известно, за расстояние
. Как известно, за расстояние 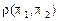 между параллельными плоскостями принимают расстояние от какой-либо точки одной плоскости до другой плоскости. Используя только что полученную формулу, нетрудно показать, что
между параллельными плоскостями принимают расстояние от какой-либо точки одной плоскости до другой плоскости. Используя только что полученную формулу, нетрудно показать, что 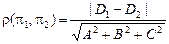 .
.
Как известно, углом между прямой и плоскостью в случае, когда прямая и плоскость не перпендикулярны, называется любой из двух смежных углов между прямой и её проекцией на плоскость.
 Теорема 5. Пусть
Теорема 5. Пусть 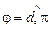 , плоскость
, плоскость 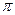 задана уравнением
задана уравнением 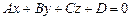 , а прямая d-уравнением
, а прямая d-уравнением 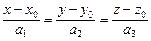 . Тогда
. Тогда 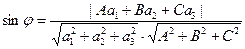 .
.
Рассмотрим вопрос о взаимном расположении прямой d и плоскости p.
Теорема 6. Пустьплоскость p заданная уравнением 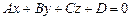 , а прямая d- уравнением
, а прямая d- уравнением 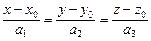 . Тогда:
. Тогда:
1) d лежит в плоскости p Û 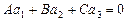 ,
, 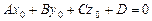 .
.
2) 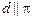 (т.е. не имеют общих точек) Û
(т.е. не имеют общих точек) Û 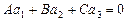 ,
, 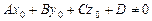 .
.
3) d пересекает p (т.е. имеет с p одну общую точку) Û  .
.
4) плоскость p прямая d взаимно перпендикулярны 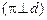 Û
Û 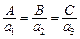 .
.
Дата публикования: 2015-09-18; Прочитано: 281 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
