Скалярное произведение векторов

Определение 1. Скалярным произведением любых двух векторов а и b называется число , где -угол между этими векторами.

К понятию скалярного произведения мы приходим, изучая работу постоянной силы, действующей на прямолинейно перемещающуюся точку 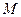. Как известно из физики, работа силы 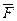на перемещении определяется равенством , где -угол, который составляет сила 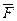с перемещением точки .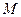

Условимся считать, что нулевой вектор перпендикулярен любому вектору.

Теорема 1.

1) (а и b перпендикулярны);

2) j – острый;

3) j – тупой;

4) , = 0.

Теорема 2(Законы скалярного произведения).

1) (коммутативность);

2) (однородность);

3) (аддитивность).

Свойства 2) и 3) называются линейностью скалярного произведения по первому аргументу. Нетрудно видеть, что скалярное произведение векторов линейно также и по второму аргументу, т.е.

Введём теперь СК OXYZ. Очевидно, для ортов координатных осей справедливы равенства:

Используя эти равенства и линейность скалярного произведения векторов как по первому, так и по второму аргументам, получаем следующую теорему.

Теорема3. Пусть 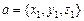, 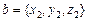. Тогда

.

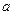Следствие 1. Пусть -угол между векторами и 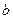, каждый из которых отличен от нуля. Тогда

.