Смешанное произведение векторов

Рассмотрим упорядоченную тройку векторов .

Определение1. Смешанным произведением векторов называется число, определяемое следующим образом: , т.е. векторно перемножаем а и b и полученный вектор скалярно умножаем на вектор с.

Смешанное произведение есть скаляр. Выясним его геометрический смысл.

Определение 2. Пусть -упорядоченная тройка некомпланарных векторов. Приложим их к одной точке и построим параллелепипед, образующими рёбрами которого будут векторы . Если тройка векторов – правая (левая), то и параллелепипед будем называть правоориентированным (левоориентированным).

Определение 3. Объёмом ориентированного параллелепипеда, построенного на векторах , называется число, обозначаемое , и равное объёму этого параллелепипеда, взятому со знаком плюс, если тройка – правая, и со знаком минус, если тройка векторов левая.

Геометрический смысл смешанного произведения даёт следующая

Теорема 1. = .

Наряду с параллелепипедом можно рассматривать ориентированный тетраэдр, и тогда для объёма 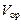ориентированного тетраэдра будет справедлива формула .

Введём прямоугольную СК ОXYZ.

Теорема 2. Пусть 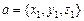, , 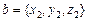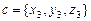.Тогда

,

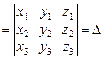т.е. смешанное произведение векторов равно определителю матрицы, строками которой являются координаты векторов . Знак определителя определяет ориентацию тройки: "+" – правая, "–" – левая ориентация.

Следствие 1. Векторы компланарны тогда и только тогда, когда их смешанное произведение равно 0.

Теорема 3 (Свойства смешанного произведения).

1. С мешанное произведение не меняется при круговой перестановке векторов:

.

2. Перестановка любых двух векторов меняет знак смешанного произведения:

.

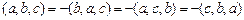3. Смешанное произведение линейно по каждому аргументу. Например, по второму:

.

4. (смешанное произведение ассоциативно относительно операции векторного произведения).

Действительно, с учётом свойства 1, имеем .