 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Угол между двумя прямыми на плоскости
|
|
Определение 1. Углом между двумя прямыми на плоскости называется угол между любыми направляющими векторами этих прямых. 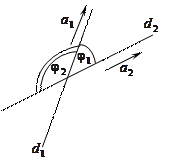
Согласно этому определению каждый из двух смежных углов 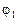 и
и 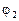 является углом между прямыми
является углом между прямыми 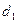 и
и 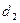 . Если прямые заданы общими уравнениями:
. Если прямые заданы общими уравнениями: 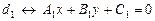 ,
, 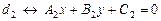 , то взяв за направляющие векторы
, то взяв за направляющие векторы 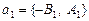 и
и 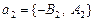 , получаем формулу
, получаем формулу
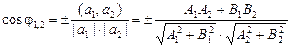 .
.
Поэтому:
1) прямые 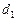 и
и 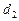 перпендикулярны Û
перпендикулярны Û 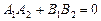 ;
;
2) если прямые 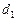 и
и 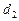 заданы угловыми коэффициентами
заданы угловыми коэффициентами 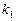 и
и 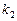 , то они будут перпендикулярны Û
, то они будут перпендикулярны Û 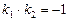 .
.
30) Взаимное расположение прямых на плоскости.
Пусть прямые 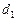 и
и 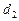 заданы уравнениями
заданы уравнениями 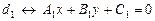 и
и 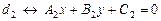 .
.
Теорема 1.1) Прямые 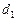 и
и 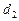 параллельны Û
параллельны Û 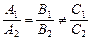 .
.
2) 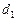 и
и 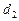 пересекаются Û
пересекаются Û 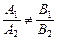 .
.
3) 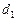 и
и 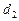 совпадают Û
совпадают Û 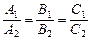 .
.
Дата публикования: 2015-09-18; Прочитано: 931 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
