Различные уравнения прямой на плоскости

Определение 1. Всякий ненулевой вектор, параллельный прямой d, будем называть направляющим вектором этой прямой.

Очевидно, что у прямой имеется бесчисленное множество направляющих векторов, состоящее из всех ненулевых векторов, коллинеарных какому либо направляющему вектору прямой. Если прямая задана уравнением Ax+By+C= 0, где , то вектор будет направляющим вектором этой прямой.

Определение 2. Вектор 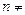0 называется перпендикулярным прямой, если он перпендикулярен направляющему вектору этой прямой.

Если прямая задана уравнением Ax+By+C= 0, где , то вектор будет перпендикулярен этой прямой.

Прямая может быть задана:

1) точкой и направляющим вектором а;

2) любыми двумя своими различными точками и ;

3) точкой и вектором 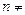0, перпендикулярным прямой.

1) 2) 3)

Пусть прямая задана точкой и направляющим вектором . Тогда для любой точки на прямой .

Записав последнее условие через отношение координат, мы получим каноническое уравнение прямой: .

Если мы условие запишем в виде , где t пробегает всё множество вещественных чисел , то получим параметрические уравнения прямой:

.

Если прямая задана двумя своими различными точками , , то за направляющий вектор можно взять вектор 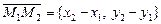. Подставив в каноническое уравнение эти данные, получим уравнение прямой, проходящей через две заданные точки и : .

Пусть теперь , – точки пересечения прямой с осями ОХ и ОY соответственно, подставляя координаты точек А и В в уравнение прямой, заданной двумя точками, получим уравнение 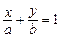, называемое уравнением прямой в отрезках.

Если прямая задана точкой и вектором 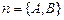, перпендикулярным прямой, то для любой точки на прямой вектор , т.е. , откуда получаем уравнение прямой, проходящей через данную точку перпендикулярно данному вектору: .

Допустим, что прямая, общее уравнение которой есть Ax+By+C= 0, не параллельна оси ОY. Тогда Разделив на 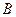, мы запишем уравнение этой прямой в виде Такое уравнение прямой называется уравнением прямой с угловым коэффициентом. В этом уравнении , где есть угол, на который надо повернуть положительную полуось ОХ до совмещения с данной прямой, а 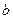есть ордината точки пересечения данной прямой с осью ОY.