Базис на плоскости и в пространстве

Определение 1. Упорядоченная система линейно независимых векторов, лежащих на данной прямой (в данной плоскости, пространстве), называется базисом на этой прямой (на этой плоскости, в пространстве), если любой вектор, лежащий на данной прямой (в данной плоскости, пространстве) представим в виде линейно комбинации векторов этой линейно независимой системы.

Теорема 1. Любой ненулевой вектор, лежащий на данной прямой, образует базис на этой прямой.

Теорема 2. Любая пара неколлинеарных векторов, лежащих в данной плоскости, образует базис на этой плоскости.

Теорема 3. Любая тройка некомпланарных векторов образует базис в пространстве.

Определение 2. Представление вектора в виде линейной комбинации элементов некоторого базиса называется разложением данного вектора по этому базису. Если базис и , то числа называются координатами вектора 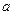в данном базисе.

Теорема 4. Разложение вектора по базису единственно.

Теорема 5. При сложении векторов одноименные координаты складываются. При умножении вектора на число все его координаты умножаются на это число.

Теорема 6.

1) Векторы 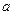и равны тогда и только тогда, когда равны их координаты.

2) Векторы 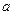и коллинеарны тогда и только тогда, когда их координаты пропорциональны.