Определение ранга матрицы. Теоремы о базисном миноре и о ранге матрицы

Рассмотрим произвольную матрицу

Определение1. Минором -го порядка матрицы называется определитель, образованный элементами, расположенными на пересечении каких-либо строк и каких-либо столбцов.

Элемент матрицы можно рассматривать как минор первого порядка.

Пример 1. Рассмотрим матрицу

.

Определитель есть минор второго порядка. Он составлен из элементов, стоящих на пересечении двух строк (1-ой и 3-ей) и двух столбцов (2-го и 3-го). Очевидно, в данной матрице миноров порядка выше третьего нет.

Вообще, если матрица имеет порядок , то наивысший порядок минора равен наименьшему из чисел и 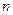, которое будет обозначаться .

Определение2. Пусть - матрица размера . Если матрица нулевая, то ее ранг равен нулю. Если матрица ненулевая, то ее рангом называется наибольшее из натуральных чисел , таких, что существует минор порядка , отличный от нуля.

Ранг матрицы будем обозначать символом . Очевидно, если существуют миноры порядка большего , то они равны нулю.

Пример 2. .

Пример 3. Вычислим ранг матрицы , используя определение ранга матрицы.

.

1) Рассмотрим миноры первого порядка матрицы : среди них есть ненулевые;

2) Существует минор второго порядка, отличный от нуля:

Поэтому ранг не равен 1.

3) Рассмотрим миноры 3-го порядка. Каждый из них лежит на пересечении всех трех строк матрицы и на пересечении каких-либо трех из четырех столбцов матрицы . Поскольку

,

то в каждом из миноров третья строка будет суммой первых двух. Поэтому все миноры третьего порядка равны нулю, и тем самым .

Определение3. Пусть - ненулевая матрица, ранг которой равен . Минор порядка , отличный от нуля, называется, базисным минором. Строки (столбцы) матрицы , на пересечении которых лежит базисный минор, называются базисными строками (столбцами).

Теорема1 (О базисном миноре).

Базисные строки (столбцы) линейно независимы. Любая строка (столбец) матрицы является линейной комбинацией ее базисных строк (столбцов).

Следствие1. Если матрица квадратная и , то столбцы (строки) матрицы образуют линейно зависимую систему.

Теорема 2 (О ранге матрицы).

Ранг матрицы равен максимальному числу ее линейно независимых строк (столбцов).