Обратимые матрицы

Определение 1. Квадратная матрица называется обратимой, если существует квадратная матрица такая, что

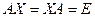(1)

Каждая матрица , удовлетворяющая (1), называется матрицей, обратной к , или обращением матрицы .

Предложение1. У каждой обратимой матрицы существует лишь одно обращение.

Обращение матрицы , если оно существует, обозначается через .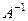

Предложение 2. .

Предложении 3. Пусть квадратные матрицы и 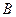обратимы и имеют один порядок. Тогда их произведение также обратимо и при этом

Предложение 4. Если матрица обратима, то транспонированная матрица также обратима, и при этом