Уравнение пучка плоскостей

Пусть уравнения данной прямой 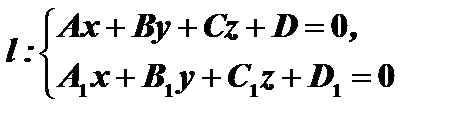. Составим уравнение первой

степени: 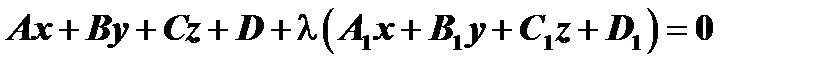, (27)

которое при любом значении постоянного 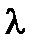определяет плоскость. Если точка лежит на данной прямой, то её координаты одновременно удовлетворяют обоим уравнениям этой прямой и, следовательно, уравнению (27) при любом значении 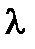. Таким образом, уравнение (27) определяет плоскости, проходящие через данную прямую. Обратно, всякая такая плоскость определяется одной точкой 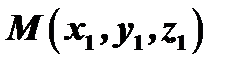, лежащей вне данной прямой линии; значение постоянного , соответствующее этой плоскости, найдётся из условия

,

если только 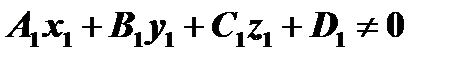. Таким образом, уравнение (27) при соответствующем выборе определяет любую плоскость, проходящую через данную прямую, за исключением лишь одной из них, именно плоскости

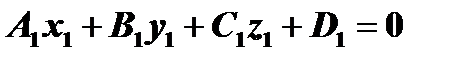
Уравнение

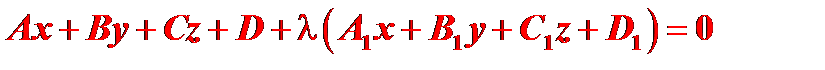(27)

называется уравнением пучка плоскостей.