Предел последовательности и функции. Свойства пределов

Одним из основных понятий математики является понятие множества. Это понятие первоначально, и его не определяют с помощью более простых понятий. Можно сказать, что множество – это семейство, совокупность, класс, система. Объекты или предметы, составляющие данное множество, называются его элементами. Если есть элемент множества 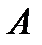, то говорят, что принадлежит и записывают . Множество называется конечным, если оно содержит конечное число элементов. Бесконечное множество называется счетным, если оно эквивалентно множеству натуральных чисел, например, счетным является множество чисел ; множество чисел, удовлетворяющих условию , не является счетным. Множество называется упорядоченным, если в нем введено отношение порядка между элементами.

Пусть счетное множество, среди элементов которого могут быть одинаковые. Сопоставим каждому элементу из свое натуральное число 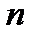и напишем это в виде индекса у соответствующего элемента ; получим 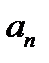. Примем число за порядковый номер элемента .

Упорядоченное счетное множество, элементы которого занумерованы и расположены в порядке возрастания номеров , называется последовательностью и обозначается символом .

Число называется пределом последовательности при стремлении к бесконечности, если для каждого положительного существует положительное число такое, что для всех выполняется неравенство . При этом пишут: .

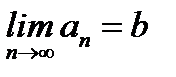Рассмотрим прежде всего следующие примеры функции: при значениях , близких к (рис.1).

Графики этих функций либо пересекают ось абсцисс, либо касаются ее в точке . В случае график расположен в области положительных ординат и только в точке касается оси абсцисс. В других случаях графики пересекают ось абсцисс и ординаты принимают значения разных знаков по обе стороны точки .

Что можно сказать о значениях функции (не о графике) в этих случаях? Ответ: значения функции сколь угодно малы по абсолютной величине, если соответствующие значения аргумента достаточно близки к .

Отвлекаясь от примеров, приходим к следующей предварительной формулировке понятия бесконечно малой функции. Функция называется бесконечно малой при стремлении к , если ее значения сколь угодно малы по абсолютной величине при всех значениях , достаточно близких к .

В дальнейшем часто будем пользоваться такими оборотами речи: «значения функции сколь угодно малы по абсолютной величине», «переменная 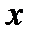принимает значения, достаточно близкие к ». Выясним их точный смысл.

Часть фразы «значения функции сколь угодно малы по абсолютной величине» будем понимать в том смысле, что неравенство выполняется для каждого наперед заданного положительного числа , как бы мало оно ни было.

Часть фразы «значения аргумента достаточно близки к » или «значения аргумента достаточно мало отличаются от числа » следует понимать в том смысле, что неравенство выполняется для некоторого положительного числа .

Определение1. Пусть функция 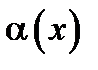определена в некоторой окрестности точки , за исключением, может быть, самой точки .

Функция 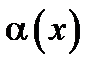называется бесконечной малой при стремлении к , если для каждого положительного сколь угодно малого 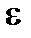существует соответствующее положительное число 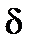такое, что выполняется неравенство для каждого , удовлетворяющего условию .

Тот факт, что является бесконечно малой при стремлении к , записывают символически так: или при .

Если функция представляется в виде суммы постоянного числа и бесконечно малой : , то 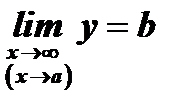. Обратно, если 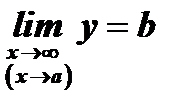, то можно записать , где бесконечно малая.

Определение2. Пусть функция определена в некоторой окрестности точки , за исключением, может быть, самой точки .

Функция называется бесконечной большой при стремлении к , если для каждого положительного как угодно большого числа существует соответствующее положительное число 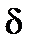такое, что выполняется неравенство 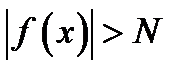для всех значений , удовлетворяющих условию .

Тот факт, что является бесконечно большой функцией при стремлении к , записывают символически так: .

Определение3. Число называется пределом функции при стремлении к , если для каждого положительного числа существует соответствующее положительное число такое, что при условии выполняется неравенство .

Если неравенство выполняется при условии , то число называется пределом справа и обозначается символом .

Если неравенство выполняется при условии , то число называется пределом слева и обозначается символом .

Основные свойства пределов:

1) ;

2) ;

3) ;

4) если переменная величина 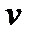возрастающая, т.е. всякое ее последующее значение больше предыдущего, и если она ограничена, т.е. , то эта переменная величина имеет предел ;

5) если между соответствующими значениями трех функции выполняются неравенства , при этом 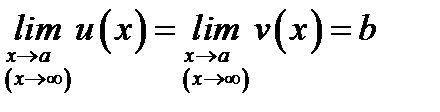, то .

Предел функци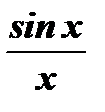и при

Функция не определена при , т.к. числитель и знаменатель дроби обращаются в нуль. Найдем предел этой функции при .

Рассмотрим окружность радиуса 1 (рис.2); обозначим центральный угол через , при этом . Из рисунка непосредственно следует:

Площадь < площади сектора < площади (1)

;

;

.

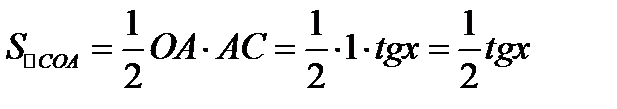Неравенства (1) после сокращения на перепишется так:

Разделив все члены на , получим или 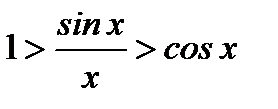. Это неравенство выведено в предположении, что ; замечая, что , заключаем, что оно верно и при . Вычислим предел

Однако 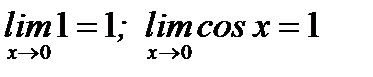и на основании свойства (5) о пределах

(2)

Предел функции при

Предварительно рассмотрим переменную величину , где возрастающая переменная величина, принимающая значения натурального ряда чисел 1, 2, 3,...

Теорема. Переменная величина при имеет предел, заключенный между числами 2 и 3.

Доказательство. По формуле бинома Ньютона имеем:

(3)

Произведя элементарные алгебраические преобразования, получим:

Из последнего равенства следует, что переменная величина возрастающая переменная величина при возрастающем .

Действительно, при переходе от значения к значению каждое слагаемое последней суммы возрастает и т.д. и добавляется еще один член.

Покажем, что эта величина ограничена. Заметим, что и т. д. Тогда

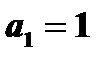Замечая, что , можем написать неравенство , но образуют геометрическую прогрессию со знаменателем и первым членом . Следовательно, ;

Получаем неравенство , т.е. переменная величина ограничена. Возрастающая и ограниченная последовательность имеет предел (п.4 свойства пределов). Этот предел обозначается буквой , таким образом,

Число иррациональное число.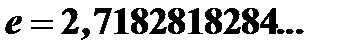

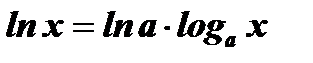Число принято за основание системы логарифмов, называемых натуральными. Натуральный логарифм обозначается символом . Установим связь между натуральными и десятичными логарифмами. Для этого, логарифмируя по основанию тождество , получим равенство . При это равенство дает . При то же равенство дает .