 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Основные правила дифференцирования. Пусть и - дифференцируемые функции
|
|
Пусть 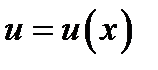 и
и 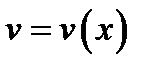 - дифференцируемые функции.
- дифференцируемые функции.
1. Постоянный множитель можно вынести за знак производной:
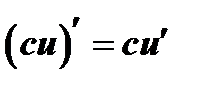
2. Производная алгебраической суммы двух дифференцируемых функций равна сумме их производных:
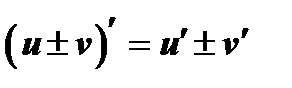
3. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго:
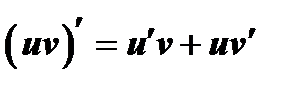
Доказательство:
а) 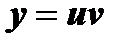 ;
; 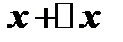
б) 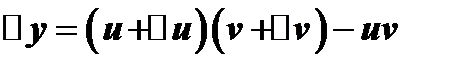
в) 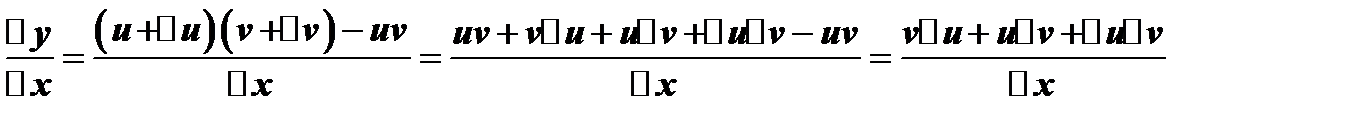
г) 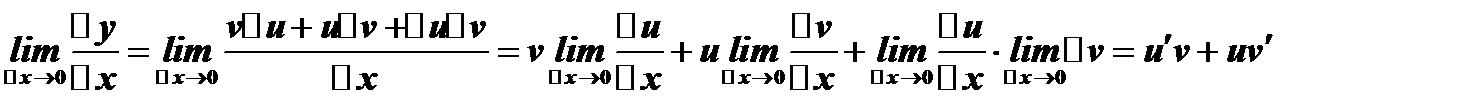 , т.к.
, т.к. 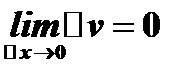 .
.
4. Производная частного двух дифференцируемых функций при 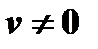 имеет следующее выражение:
имеет следующее выражение:
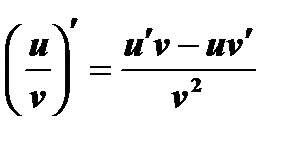
В частности: 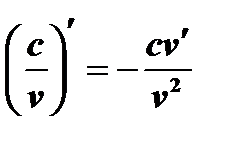 ;
; 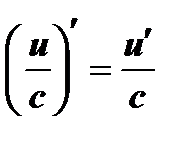 , где
, где 
5. Производная сложной функции 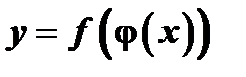 , составленной из дифференцируемых функций
, составленной из дифференцируемых функций 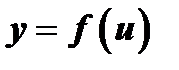 и
и 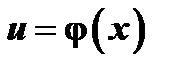 , равна произведению производной внешней функции
, равна произведению производной внешней функции 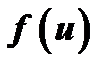 по промежуточному аргументу
по промежуточному аргументу 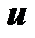 на производную этого аргумента по независимой переменной
на производную этого аргумента по независимой переменной 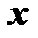 :
:
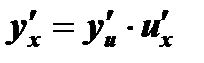
6. Если функция 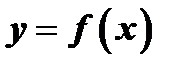 имеет при некотором значении
имеет при некотором значении 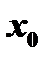 отличную от нуля производную, то обратная функция
отличную от нуля производную, то обратная функция 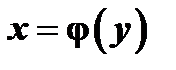 имеет в соответствующей точке
имеет в соответствующей точке 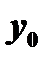 производную
производную 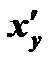 , равную единице, деленной на
, равную единице, деленной на 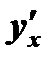 :
:
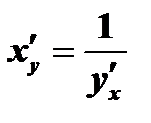
7. Пусть зависимость 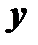 от
от 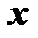 не задана непосредственно, а вместо этого задана зависимость обеих переменных
не задана непосредственно, а вместо этого задана зависимость обеих переменных 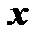 и
и 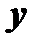 от некоторой третьей, вспомогательной, переменной (называемой параметром):
от некоторой третьей, вспомогательной, переменной (называемой параметром): 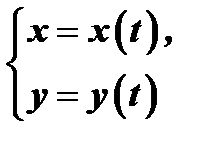
Предположим, что функция 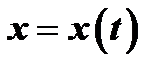 имеет обратную функцию
имеет обратную функцию 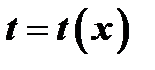 . Тогда, очевидно,
. Тогда, очевидно, 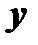 является функцией от
является функцией от 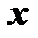 :
: 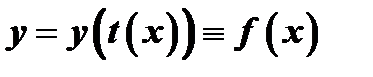 .
.
Если функции 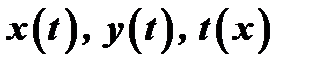 имеют производные, то и функция
имеют производные, то и функция 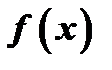 имеет производную. Действительно, по правилу дифференцирования сложной функции имеем
имеет производную. Действительно, по правилу дифференцирования сложной функции имеем 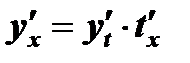 , где (согласно правилу дифференцирования обратной функции)
, где (согласно правилу дифференцирования обратной функции) 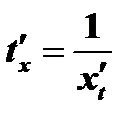 . Поэтому при
. Поэтому при 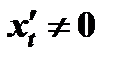 получаем окончательно
получаем окончательно
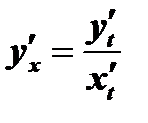
8. Пусть значения двух переменных 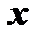 и
и 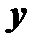 связаны между собой некоторым уравнением, которое символически обозначим так:
связаны между собой некоторым уравнением, которое символически обозначим так: 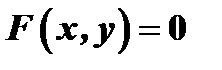 . Такое задание функции
. Такое задание функции 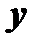 от
от 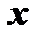 называется неявным заданием. Укажем правило нахождения производной неявной функции, не преобразовывая ее в явную, т.е. не представляя в виде
называется неявным заданием. Укажем правило нахождения производной неявной функции, не преобразовывая ее в явную, т.е. не представляя в виде 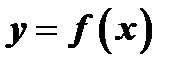 . Следует учесть, что если
. Следует учесть, что если 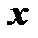 аргумент функции, то
аргумент функции, то 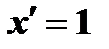 ; а если
; а если 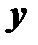 не аргумент, а функция от
не аргумент, а функция от 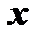 , то производная
, то производная 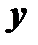 равна не единице, а
равна не единице, а 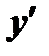 .
.
Допустим, что функция задана уравнением 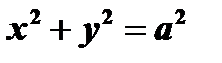 , то
, то 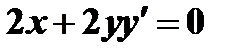 , откуда
, откуда 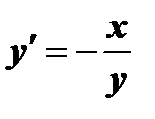 .
.
9. Сложной показательной функцией называется функция, у которой и основание и показатель степени являются функциями от 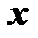 , например,
, например, 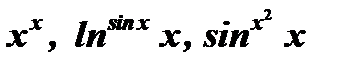 , вообще, всякая функция вида
, вообще, всякая функция вида 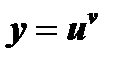 . При определении производной таких функции применяется предварительное логарифмирование.
. При определении производной таких функции применяется предварительное логарифмирование.
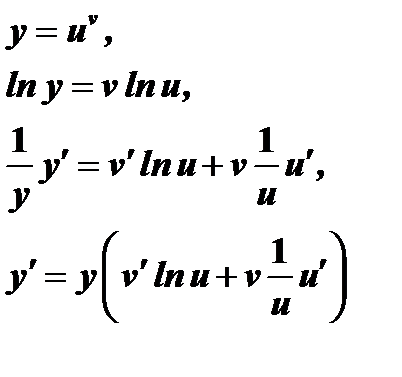
Зная, что 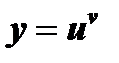 , получим
, получим 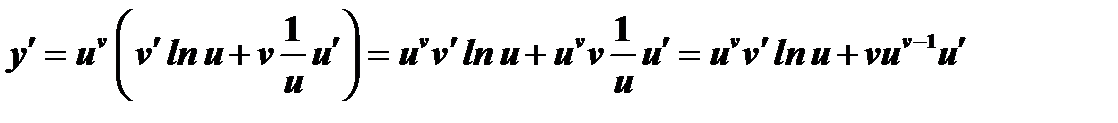
Дата публикования: 2015-09-17; Прочитано: 365 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
