 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Конструктивные свойства трёхосного эллипсоида
|
|
(рис.15.82, 15.83)
Определение 15.12. Система по-следовательных положений эллипти-ческой образующей линии а, закон из-менения длин осей которой определя-
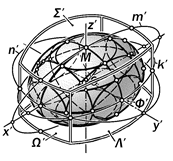
|
Рис.15.84. Геометрическая модель золотого трёхосного эллипсоида

|
Рис.15.85. Графическая модель золотого трёхосного эллипсоида
ется значениями длин соответст-вующих хорд двух конкурентных и вза-имно-перпендикулярных направляющих эллипсов b и c с общим центром О на-зывается трёхосным эллипсоидом.
Как правило, общий центр О напра-вляющих эллипсов b и с принимают за начало осей х, y и z декартовых коорди-нат, с которыми совпадают их соответ-ственные оси. Плоскость кривизны об-разующего эллипса а перемещается перпендикулярно к линии пересечения направляющих эллипсов и, пересекая их, определяет свои большую и малую оси. Роль образующего эллипса может играть любой из направляющих эллип-сов
Совершенно очевидно, что соотно-шения длин осей направляющих элли-псов могут быть как произвольными, так и наперед заданными. В частности, ес-
ли направляющий эллипс в осях хОу
является золотым, то и вся поверхно-
сть становится золотой (см. рис.15.84).
Определение 15.13. Трёхосный элли-псоид Ф, горизонтальные и профильные сечения которого являются золотыми эл-липсами,а фронтальные вписываются в золотые прямоугольники, называется зо-лотым .[ 62 ].
Центр О такого эллипсоида является началом трёх взаимно-перпендикулярных осей х, у и z, которые попарно определяют соответственно горизонтальную (хОу), фро-нтальную (хОz) и профильную (yOz) плоско-сти его симметрии.
Дата публикования: 2015-09-17; Прочитано: 287 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
