 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Изобразительные свойства ортогональных проекций параболоида вращения
|
|
(рис. 15.78)
Определителем поверхности па-раболоида вращения является линия а параболы и её действительная ось как ось вращения i.
Если ось вращения занимает гори-зонтально-проецирующее положение, то очерком горизонтальной проекции Ф1 собственно поверхности Ф парабо-лоида является окружность с1 как гори-зонтальная проекция траектории вра-щения точки С, принятой за конечную точку пароболы. Часть картинного про-странства горизонтальных проекций, ог-раниченная очерком с1, заполняется
проекциями элементов линейного кар-каса поверхности, состоящими из ради-
ально расположенных проекций конгру-энтных парабол и концентрических ок-

|
Рис.15.78. Графическая модель параболоида вращения.

|
Рис.15.79. Геометрическая модель косого винтового коноида
ружностей, изображающих её паралле-ли.
Очерком фронтальной проекции Ф2 параболоида вращения является фрон-тальная проекция а2 образующей пара-болы а в её натуральную величину, ограниченная сверху горизонтальной прямолинейной проекцией с2 траекто-рии вращения точки С.
Часть картинного пространства фронтальных проекций, ограниченная очерковыми линиями а2 и с2, заполняет-ся проекциями элементов линейного каркаса поверхности, - её параллеле-лей и меридианов.
Так как директриса параболы явля-ется её неотъемлемым элементом, то она, вращаясь, образует горизонталь-ную директрисную плоскость d, подле-жащую изображению (см. d2,d1 ).
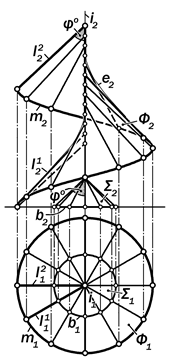
15.2.3. Конструктивные свойства косого винтового коноида и изобразительные свойства его ортогональных проекций
(рис.15. 79, 15. 80).
Определение 15.10. Кривая повер-хность Ф, образованная движением прямолинейной образующей l, пересе-кающей винтовую направляющую m и прямолинейную направляющую I под постоянным углом j°, называется ко - сым винтовым коноидом.
Для соблюдения постоянства угла j ° необходимо, чтобы образующая l была бы параллельна соответствую-щим образующим некоторой конической поверхности S с таким же углом между её образующими и осью i.
Поверхность S называется направ-ляющей, а поверхность Ф, образуемая с её помощью, относится в классу по-верхностей с направляющей поверхнос-тью.
В определитель поверхности ко-сого винтового коноида Ф входят две направляющие линии – винтовая m и ось і, образующая l и коническая по-верхность S с заданным углом j° на-клона её образующих к оси і.
Ф = [ m, i, l || (l1 Î S) ], Ð i l = j°- const..
Очерком горизонтальной проекции
Ф1 поверхности Ф является окружность
m1 горизонтальной проекции цилиндри-
ческой винтовой линии m.
Часть картины, ограниченная очер-ковой линией, заполняется равномерно расположенными 12-ю радиальными отрезками как горизонтальными проек-циями последовательных положений образующей l, а также некоторой окруж-ностью b1, изображающей основание направляющей конической поверхности S с заданным углом j° наклона её образующей к оси i.
|
Рис.15.80. Графическая модель косого винтового коноида
Очерк фронтальной проекции Ф2 по-верхности Ф складывается из несколь-ких линий: фронтальной проекции m2 направляющей винтовой линии m в ви-де одной волны синусоиды, двух фрон-тальных проекций l2 образующей l соот- ветственно в начальном и конечном положениях и очерковой линии е2, оги-бающей проекции образующих в неко-торых положениях.
Фигура очерка фронтальной проек-ции поверхности Ф заполняется проек-циями образующей в её последовате-льных положениях, параллельных со-ответствующим образующим направля-ющей поверхности S.

|
Рис.15.81. Графическая модель сложной поверхности вращения

|
Рис.15.82. Определитель поверхности
трёхосного эллипсоида

|
Рис.15.83. Геометрическая модель
трёхосного эллипсоида
Дата публикования: 2015-09-17; Прочитано: 628 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
