Проекций криволинейчатых кривых поверхностей

(рис. 15.54 – 15.64)

Общие положения

Определение 15.11. Система по-следовательных положений образую-

щей линии, которая вращается вокруг

Рис.15.54. Геометрическая модель од-нополостного гиперболоида вращения

Рис.15.55. Геометрическая модель сферической поверхности

Рис.15.56 Геометрическая модель закрытого тора

Рис.15.57. Геометрическая модель открытого тора

прямолинейной неподвижной оси, назы-

вается поверхностью вращения.

Ф = (l, і)

Вполне очевидно, что вид образуе-мой поверхности определяется видом вращающейся образующей.

1. Если образующая линия прямая, то образуемая ею поверхность вра-щения является прямолинейчатой. Её вид зависит от положення образующей по отношению к оси вращения:

1.1. Если прямолинейная образую-щая паралельна оси вращения, то она образует поверхность прямого круго-вого цилиндра (см. рис.15. 18).

1.2. Если прямолинейная образую-щая, вращаясь вокруг оси, пересекает её, то она образует поверхность пря-мого кругового конуса (см. рис. 15.15)

1.3. Если прямолинейная образую-щая, вращаясь вокруг оси, скрещивает-ся с нею, то она образует поверхность однополостного гиперболоида враще-ния (рис. 15. 54).

2. Если образующая линия кривая, то образуемая ею поверхность враще-ния является криволинейчатой и её вид определяется видом этой кривой, а также её положением относительно оси вращения.

Так как точки образующей линии в общем случае удалены от оси враще-ния на разные расстояния, то, враща-ясь, они описывают в пространстве ок-ружности разного радиуса. Эти окруж-ности называются паралелями образуе-мой поверхности вращения. Параллель наибольшего радиуса называется её экватором, а паралель наименьшего радиуса,- горловиной или горлом.

Линии, определяемые точками пе-ресечения паралелей поверхности вра-щения плоскостями, приходящими че-рез её ось, называются её меридиана-ми. Меридианы, которые лежат в плос-костях уровня, являются главными. Все меридианы поверхности вращения между собою конгруэнтны.

Утверждение 15.5. Линейный кар-кас любой поверхности вращения яв-ляется системой её конкурентних паралелей и меридианов.

Образующие кривые линии могут быть закономерными и незакономерны-

ми, плоскими и пространственными, по разному расположенными относитель-

но оси вращения. Этим определяется большое разнообразие видов поверх-ностей вращения, обладающих различ-ными конструктивними особенностями, но образуемые по одним и тем же гео-метрическим законам.

Наиболее простой и наиболее рас-пространённой кривой линией является окружность.

2.1. Если окружность вращается во-круг любого из своих диаметров, то она образует сферическую поверхность (рис.15. 55).

2.2. Если окружность вращается во-круг одной из свои хорд, то она образу-ет поверхность закрытого тора (рис. 15.56).

2.3. Если окружность вращается во-круг неконкурентной, но компланарной с

нею прямой, то она образует поверхно-

сть открытого тора (рис. 15. 57).

2.4. Если окружность вращается во-круг неконкурентной и некомпланарной с нею прямой, то она образует поверх-ность глобоида (рис.15. 58).

Рис.15.58. Геометрическая модель глобоида

Окружность является частным слу-чаем эллипса, у которого большая ось равна малой. Если эллипс принимать за образующую линию, то с её помощью можно образовать поверхности враще-ния, родственные тем, которые получа-ются вращением окружности (см.п.п. 2.1- 2.4). Однако наиболее распростра-нёнными являются поверхности, полу-чаемые вращением эллипса вокруг его осей.

2.5. Если эллипс вращается вокруг его большой оси, то он образует повер-

хность сжатого эллипсоида вращения

(рис.15. 59).

Рис.15.59. Геометрическая модель сжатого эллипсоида вращения

Рис.15.60. Геометрическая модель поверхности растянутого эллипсоида

Рис.15.61. Геометрическая модель поверхности параболоида вращения

2.6. Если эллипс вра-щается вокруг его малой оси, то он образует пове-

рхность рас тягнутого эл-липсоида вращения (рис. 15. 60).

Так как директрисы эл- липса являються его неот-ъемлемыми элементами, то, вращаясь вместе с ним, у сжатого эллипсоида образуются две параллельные директрисные плоскости d и g, а у растянутого – соосная с ним цилиндрическая директрисная поверх-ность S.

2.7.Если образующая линия явля-

ется параболой, то, вращаясь вокруг своей оси симметрии, она образует па-

раболоїд вращения, дополняемый ди-

ректрисной плоскостью d (рис. 15.61).

2.8. Если образующая линия является гиперболой, то вра-щаясь вокруг мнимой оси сим-метрии, она образует поверхность

однополостного гиперболоида вращения, дополненного повер- хностью двуполостного асимпто-

тического конуса D и конкурентной

с неё соосной поверхностью ди-ректрисного цилиндра S.(рис. 15. 62).

2.9. Вращаясь вокруг действитель-ной оси симметрии, гипербола обра-зует поверхность двупололос тного гиперболоида вращения, дополненного поверхностью асимптотического конуса и двумя конкурентними с ней дирек-трисными плоскостями (рис.15. 63).

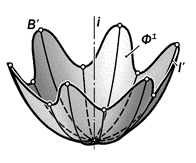
2.10. Если произвольной формы

плоская образующая кривая в процес-се вращения вокруг пересекающей её оси изменяет свою форму по опреде-лённому периодическому закону, то она образует сложную поверхность враще-ния (рис. 15. 64).

15.2.2. Изобразительные свойства ортогональных проекций поверхностей вращения

(рис. 15.65 -15.78, 15.81)

Общие положения

Так как все поверхности вращения, независимо от формы их образующих,

образуются по одному и тому же прин-

Рис.15.62 Геометрическая модель поверхности однополостного гиперболоида вращения

Рис.15.63. Геометрическая модель поверхности двуполостного гиперболоида вращения.

Рис.15.64. Геометрическая модель сложной поверхности вращения

ципу, то на особенности изобразитель-

ных свойств их ортогональных проек-ций оказывает влияние только лишь по-ложение оси вращения по отношению к плоскостям проекций.

Как правило, эта ось, для наиболее простого построения, располагается в проецирующем положении, реже, - в по-

Рис. 15.65. Графическая модель поверхности вращения произвольного

вида

Рис.15.66. Графическая модель одно-полостного гиперболоида вращения, ось которого горизонтальна

ложении линии уровня, и очень редко, - в общем положении.

1. Если ось вращения занимает го-ризонтально-проецирующее положе-ние, то:

1.1. очерк её горизонтальной проек-ции определяется двумя окружностями, которые изображают самую большую (экватор) и самую малую (горловину) параллели;

Рис. 15.67. Графическая модель

однополостного гиперболоида вращения,

ось которого фронтальна

1.2. очерк её фронтальной проекции

определяется фронтальной проекцией её главного меридиана. Если поверх-ность прямолинейчатая, то очерком её фронтальной проекции является кри-вая, огибающая последовательные по-

ложения фронтальных проекций обра-

зующей (рис.15.65).

2. Если ось вращения занимает

фронтально-проецирующее положение,

то очерк её фронтальной проекции по-добен очерку горизонтальной проекции поверхности с вертикальной осью (см. п.1.1), и наоборот, структура очерка ее горизонтальной проекции подобна оче-рку фронтальной проекции такой пове-рхности (см. п.1.2).

3. Если ось вращения занимает в пространстве положение линии уровня,

то необходимо (рис.15.66, 15.67):

3.1. одним преобразованием пере-вести её в проецирующее положение, построить вспомогательную проекцию в виде окружностей экватора, горловины и промежуточных параллелей,

3.2.по вспомогательной проекции

построить первую искомую проекцию поверхности на ту плоскость, по отно-шению к которой её ось параллельна (см. п.1.2);

3.3. по первой искомой проекции построить её вторую искомую проек-цию, промоделировав все инциденции изображаемой поверхности.

4. Если ось вращения занимает в пространстве общее положение, то не-обходимо (рис.15:68):

4.1. на ортогональных проекциях оси общего положения выделить необ-ходимое число точек-центров окружно-стей-параллелей поверхности разного радиуса,

4.2. через проекции выделенных точек провести проекции плоскостей, перпендикулярные к оси и задаваемых их линиями уровня;

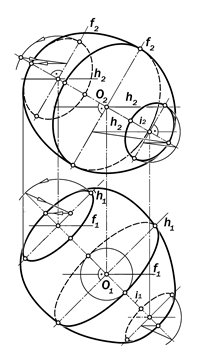
Рис.15.68. Графическая модель поверхности вращения, ось которой занимает в пространстве

общее положение

4.3. по графическому алгоритму ри-сунка 12.43 построить проекции окруж-

ностей разного радиуса в виде соот-ветственно подобных эллипсов;

4.4. Под лекало провести плав-ные очерковые линии, огибающие проекции

Рис.15.69. Графическая модель одно-польстного гиперболоида, образованно-го вращением прямой линии

Рис. 15.70. Графическая модель одно-полостного гиперболоида, образованно-го вращением гиперболы вокруг её мнимой оси

параллелей и симметричные относите-льно соответствующих проекций оси вращения.