Теоретические сведения. Рассмотрим функцию f(x), определенную на промежутке xÎ(a,b)

Рассмотрим функцию f(x), определенную на промежутке x Î(a,b). Характер поведения функции в области определения можно исследовать, опираясь на следующие утверждения:

• Если f(x ₀ ) =0, то график функции пересекает ось абсцисс в точке x ₀;
• Если 0Î(a,b), то график функции пересекает ось ординат в точке y ₀= f( 0 );
• Если в точке x ₀Î(a,b) функция имеет бесконечный разрыв, то график функции имеет вертикальную асимптоту x = x ₀;
• Если (a,b)=(–¥, ¥), (a,b)=(а, ¥) или (a,b)=(–¥, b), существуют и конечны пределы 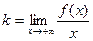и 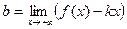то прямая y=kx+b является асимптотой графика функции при x ®¥; аналогично находят асимптоту при x ® –¥;
• Если 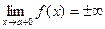, то график функции имеет на левой границе области определения вертикальную асимптоту x = а. Аналогично, если 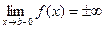, то график функции имеет на правой границе области определения вертикальную асимптоту x = b;
• Если (a,b)=(–¥, ¥) и существует такое число Т ¹0, что f (x+T)= f (x) для любого x Î(–¥, ¥), то исследуемая функция периодична с периодом Т; в этом случае достаточно построить график функции на промежутке (0, Т) и доопределить его по периодичности на всю числовую ось;
• Если f(–x) = f(x) для любого x Î(– a, a), то исследуемая функция четная. В этом случае ее график симметричен относительно оси ординат; достаточно построить график функции на промежутке (0, а) и отобразить его симметрично относительно оси ординат на промежуток (– а, 0);
• Если f(–x) = – f(x) для любого x Î(– a, a), то исследуемая функция нечетная. В этом случае ее график симметричен относительно начала координат; достаточно построить график функции на промежутке (0, а), а затем отобразить его на промежуток (– а, 0) симметрично относительно начала координат;
• Для того, чтобы дифференцируемая на (a,b) функция не убывала (не возрастала) на этом промежутке, необходимо и достаточно, чтобы 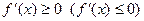на (a,b);
• Пусть 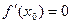. Если существует некоторая окрестность U (x ₀) точки x ₀ такая, что 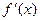меняет знак с минуса на плюс при переходе через точку x ₀, т.е. 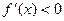, x < x ₀, 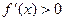, x > x ₀, x Î U (x ₀), то точка x ₀ – точка локального минимума. Если 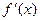меняет знак с плюса на минус при переходе через точку x ₀, т.е. 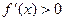, x < x ₀, 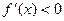, x > x ₀, x Î U (x ₀), то точка x ₀ – точка локального максимума. Если же 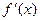не меняет знак при переходе через точку x ₀, то в этой точке локального экстремума нет. Это условие применимо также и в том случае, когда функция f(x) дифференцируема в окрестности U (x ₀), но в самой точке x ₀ её не существует;
• График функции f(x) называется вогнутым (выпуклым вниз) на промежутке (а,b), если он расположен выше касательной, проведенной в любой точке (х, f(х)), x Î(a,b). Если же график функции лежит ниже касательной, то он называется выпуклым (выпуклым вверх).
• Если дважды дифференцируемая на промежутке (a,b) функция f(x) имеет на нем положительную вторую производную, то функция вогнута на (a,b). Если же вторая производная отрицательна на промежутке (a,b), то функция на нем выпукла;
• Если вторая производная равна нулю в точке х ₀, а слева и справа от нее имеет значения разных знаков, то точка х ₀ – точка перегиба функции.

Для решения уравнений вида f(x) =0 в MathCAD можно использовать встроенную функцию root(f(x),x,a,b). Первый аргумент – функция, нуль которой необходимо найти, второй – переменная, по которой ищется решение. В общем случае функция f может быть функцией многих переменных, поэтому необходимо задавать переменную, по которой ищется корень уравнения. Третий и четвертый аргументы – границы отрезка, на котором ищется решение. Допускается использование функции root без третьего и четвертого аргумента, т.е. без задания границ отрезка поиска. Перед функцией root необходимо задать точку начального приближения, от которой ведется поиск корня.

В случае, если используется формат задания функции root с четырьмя аргументами, то на концах отрезка [a,b] значения функции f должны иметь разные знаки, то есть должно выполняться условие: f(a) ∙ f(b) <0. При этом функция root возвратит значение корня, принадлежащее данному отрезку. Если на указанном отрезке имеется несколько корней, то функция root возвратит один из них.

В случае, если используется функция root с двумя аргументами (необязательные параметры a,b опущены), то функция root возвратит значение корня, ближайшее к указанной точке начального приближения.

Точность вычислений с помощью функции root может регулироваться встроенной переменной TOL. Она задается на закладке Built-In Variables формы, которая открывается при выборе пункта меню Tools/Worksheet Options, и по умолчанию равна 0.001. Ее значение также можно изменить непосредственно в тексте документа, набрав, например: TOL: = 10^–9.

Проведем теперь краткое аналитическое исследование функции 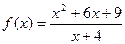и построим ее график (рисунок (12)).

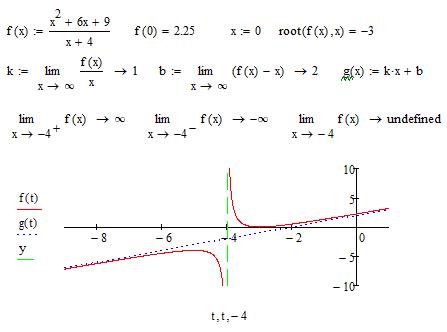
Рис. 12. Графики функции f (x) и ее асимптот.

Таким образом, у данной функции имеются две асимптоты: наклонная асимптота 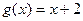и вертикальная асимптота в точке разрыва функции x = –4. Функция пересекает ось ординат в точке y = 2.25 и касается оси абсцисс в точке x = –3.

Рассмотрим пример применения дифференциального исчисления для нахождения точек экстремума функции (см. рисунок 13).

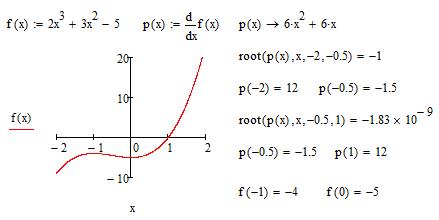
Рис. 13. Нахождение экстремумов функции f (x).

Теперь используем вторую производную для нахождения интервалов выпуклости/вогнутости функции и точек ее перегиба.

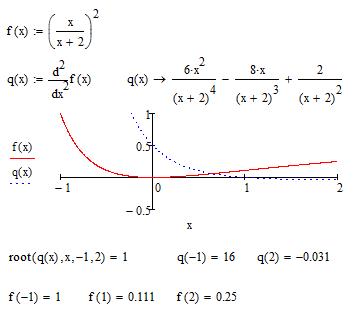
Рис. 14. Нахождение точек перегиба функции f (x).

На рисунке 14 выведены графики функций f (x) и 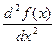, иллюстрирующие понятия выпуклости/вогнутости функции и задающие положение ее точки перегиба.