Аналітичне задання інверсії та деякі інші її властивості

Виведемо співвідношення, які зв’язують координати довільної точки та її образу при інверсії . Для цього виберемо початок прямокутної декартової системи координат у точці 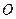. Нехай – координати точки 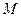, а – координати інверсної до неї точки 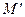, а також 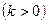. Оскільки виконуються рівності

, (2)

то

,

звідки . Тепер співвідношення (2) набувають вигляду

(3)

і дають можливість, знаючи координати точки 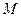, знаходити координати інверсної до неї точки 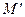. Назвемо одержані співвідношення формулами інверсії.

Оскільки образом точки 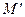при інверсії є точка 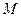, то рівності (3) можна також представити у вигляді

. (4)

Порівнюючи співвідношення (3), (4) із формулами афінних перетворень, можна зробити висновок, що інверсія не є афінним перетворенням.

Перейдемо до дослідження образів деяких геометричних фігур при перетворенні інверсії.

Теорема 1. Пряма, яка проходить через центр інверсії, при інверсії відображається на себе. Пряма, яка не проходить через центр інверсії, при інверсії відображається на коло, яке проходить через центр інверсії.

Доведення. Нехай задана пряма 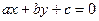. Використовуючи рівності (4), знайдемо рівняння образу даної прямої. Дістаємо , або

.

При одержана рівність визначає пряму, яка проходить через початок координат, тобто через центр інверсії.

Якщо , то, записавши одержане співвідношення у вигляді

,

переконуємось у тому, що воно визначає коло, яке проходить через центр інверсії.

Якщо пряма перетинає коло інверсії, але не проходить через його центр, то для побудови інверсного до неї кола використовують ці дві точки перетину та точку 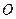, які належать шуканому колу (рис. 2).

Якщо пряма дотикається до кола інверсії у деякій точці 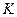, то інверсним до прямої буде коло з діаметром (рис. 3).

У випадку, коли пряма не перетинає коло інверсії, через точку 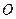проводять пряму перпендикулярно до заданої прямої. Нехай вони перетинаються у деякій точці 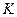. Дальше для точки 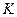будується інверсна до неї точка та на діаметрі будується інверсне до прямої коло (рис. 4).

Теорема 2. Коло, яке проходить через центр інверсії, відображається на пряму, яка не проходить через центр інверсії. Коло, яке не проходить через центр інверсії, відображається на коло, яке не проходить через центр інверсії.

Доведення. Доведення першої частини теореми випливає з попередньої теореми та властивості 5).

У випадку кола, яке не проходить через центр інверсії, виберемо вісь так, щоб вона проходила через центр кола. Тоді його рівняння можна записати у виді , причому . Використавши рівності (4), дістаємо рівняння інверсної фігури у вигляді

або

,

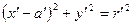де , . Оскільки при дістаємо, що , то одержане рівняння визначає коло, яке не проходить через центр інверсії. Теорема доведена.

Для побудови кола, яке інверсне до заданого, можна знайти образи трьох точок заданого кола, або побудувати дві точки, які інверсні до кінців діаметра заданого кола. У випадку, коли задане коло має із колом інверсії спільні точки, їх можна використати при побудові шуканого інверсного кола, оскільки вони належать цьому колу (на рис. 5 – це точки та ). Потрібно розуміти, що центри інверсних кіл не є інверсними точками, тому шукати центр інверсного кола, як образ центра заданого кола є помилкою.

Зауважимо, що існують чисто геометричні доведення теорем 1 та 2. Їх можна знайти, наприклад, у посібнику .

Кутом між двома лініями у деякій точці їх перетину називають кут між дотичними до цих ліній, які проведені у даній точці.

Два кола називають ортогональними, якщо вони перетинаються під прямим кутом.

Для побудови кола, ортогонального до заданого, достатньо у довільній точці кола провести дотичну, яка, очевидно, буде перпендикулярною до радіуса, проведеного у точку дотику. Коло з центром у довільній точці дотичної, яке проходить через точку дотику, буде ортогональним до заданого кола.

Теорема 3. Коло, ортогональне до кола інверсії, переходить при інверсії у себе.

Доведення. Нехай коло з центром у точці ортогональне до кола інверсії 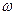з центром у початку координат та радіусом , а також точка – одна із двох точок перетину даних кіл (рис. 6). Із прямокутного трикутника дістаємо , або , де – радіус кола . Використавши останнє співвідношення та рівності , , отримані при доведенні теореми 2, дістаємо . Отже, коло , ортогональне до кола інверсії 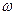, переходить при інверсії у себе.

Теорема 4. При інверсії зберігаються кути.

Доведення. Нехай дві лінії перетинаються у деякій точці та утворюють кут , а також рівняння дотичних, проведених у цій точці, мають вид : та : (рис. 7).

Очевидно, що . При інверсії дані лінії перейдуть у деякі інші лінії, кут між якими буде визначатися, як кут між дотичними до цих ліній, або кут між образами дотичних та , якими, як ми знаємо, будуть прямі або кола. Знайдемо рівняння образів дотичних. Дістаємо

,

або

.

Диференціюючи одержані рівності, знаходимо

,

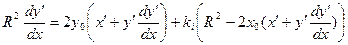звідки

.

Обчисливши значення знайдених похідних у точці , яка є інверсною до точки 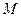, тобто при , , знаходимо кутові коефіцієнти

інверсних напрямків. Тепер знайдемо кут 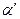між ними. Для спрощення перетворень введемо заміни . Після нескладних перетворень дістаємо

= ,

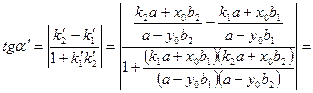
звідки випливає, що .

Зауважимо, що перетворення площини, при яких зберігаються кути, називаються конформними.