Гомотетія. Означення. Способи задання

Нехай задане деяке дійсне число , а також на площині зафіксована довільна точка 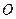. Кожній точці 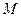площини поставимо у відповідність точку таку, що

. (1)

Оскільки при побудованій таким чином відповідності кожна точка має єдиний образ і різні точки мають різні образи, то введене правило задає перетворення площини. Таке перетворення площини називають гомотетією і позначають символом . Точку 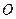називають центром гомотетії, а число – коефіцієнтом гомотетії.

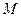При вектори та напрямлені однаково, тому точки та 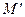лежать по одну сторону відносно точки .

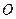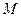При вектори та напрямлені протилежно, тому точки та 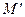лежать на прямій, яка містить точку 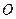, але по різні сторони відносно неї (рис. 1).

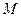При виконується рівність , тому точки та 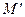співпадають. Отже, гомотетія з коефіцієнтом є тотожнім перетворенням.

При із умови (1) дістаємо, що . Одержана рівність означає, що точки 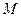та 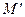розташовані симетрично відносно точки 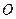. Тому гомотетія з коефіцієнтом є центральною симетрією з центром у точці .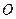

Нехай задані дві гомотетії та із спільним центром у точці 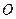та коефіцієнтами і , а також та . Оскільки виконуються рівності та , то 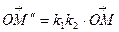. Таким чином, композиція двох гомотетій із спільним центром та коефіцієнтами та є гомотетією із тим же центром та коефіцієнтом , тобто .

Із рівності (1) дістаємо , тобто перетворення, яке є оберненим до гомотетії , теж є гомотетією з тим же центром та коефіцієнтом : . Сказане вище дозволяє стверджувати, що множина всіх гомотетій із спільним центром утворює групу.

Виберемо на площині довільну афінну систему координат 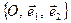з початком у точці, яка є центром гомотетії, та розглянемо точку 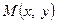. Якщо точка є гомотетичною до точки , то із рівності (1) випливає, що

. (2)

Одержані співвідношення є частинним випадком формул

,

які визначають афінні перетворення (лекція 27), тому можна стверджувати, що група гомотетій є підгрупою групи афінних перетворень та володіє всіма властивостями останньої.

Якщо центр гомотетії розташувати у деякій точці 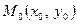, відмінній від початку координат, то формули (2) набудуть виду

. (3)

Для того, щоб у цьому переконатися, достатньо прирівняти координати векторів в обох частинах рівності .

Використаємо співвідношення (2) та (3) для того, щоб дати відповідь на питання, яке перетворення являє собою композиція двох осьових симетрій з центрами у різних точках?

Нехай задані дві гомотетії з коефіцієнтами та . Виберемо центр першої із них у початку координат (точці 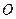), а центр другої - у точці 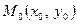. Нехай образом точки 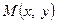при гомотетії буде точка , а образом точки при гомотетії буде точка . Оскільки при цьому будуть виконуватись рівності

та ,

то

,

звідки

. (4)

Нехай . Тоді, перетворивши одержані рівності до вигляду

(5)

та порівнявши їх із (3), можна зробити висновок, що , де точка - центр гомотетії, яка є композицією двох заданих. Очевидно, що ця точка належить прямій .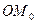

При , коли співвідношення (5) втрачають зміст, рівності (4) набувають вигляду

та, очевидно, задають паралельне перенесення.