 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Властивості рухів
|
|
Позначимо множину всіх рухів через  та нехай
та нехай  . Очевидно, що:
. Очевидно, що:
1) композиція двох переміщень, тобто перетворення  , теж є рухом;
, теж є рухом;
2) перетворення, обернене до руху, є рухом.
Справді, нехай рух  переводить відрізок
переводить відрізок  у рівний йому відрізок
у рівний йому відрізок  , а рух
, а рух  переводить відрізок
переводить відрізок  у рівний йому відрізок
у рівний йому відрізок  . Тоді, оскільки
. Тоді, оскільки 
 , то при перетворенні
, то при перетворенні  зберігаються відстані між точками.
зберігаються відстані між точками.
Із умов 1), 2) випливає, що множина всіх рухів утворює групу. Позначимо її через  . Ця група є підгрупою групи афінних перетворень.
. Ця група є підгрупою групи афінних перетворень.
У попередній лекції ми домовилися у випадку  афінне перетворення називати власним, а при
афінне перетворення називати власним, а при  – невласним. Якщо афінне перетворення є рухом, то при
– невласним. Якщо афінне перетворення є рухом, то при  це власне перетворення називають рухом першого роду, а при
це власне перетворення називають рухом першого роду, а при  – рухом другого роду.
– рухом другого роду.
Пропонуємо самостійно обґрунтувати ті факти, що тотожне перетворення є рухом першого роду, композиція двох рухів першого роду або двох рухів другого роду є рух першого роду, а композиція двох рухів різного роду є рух другого роду. Перетворення, обернене до руху першого роду, є рухом першого роду. Тому рухи першого роду утворюють підгрупу групи рухів. Множина рухів другого роду групи не утворює, оскільки композиція двох рухів другого роду не є рухом другого роду.
Група рухів, будучи підгрупою групи афінних перетворень, володіє всіма властивостями останньої. Тому:
1) при русі вектор  переходить у вектор
переходить у вектор  з такими ж координатами, зокрема колінеарні вектори відображаються у колінеарні (зауважимо, що координати векторів розглядаються відносно різних базисів);
з такими ж координатами, зокрема колінеарні вектори відображаються у колінеарні (зауважимо, що координати векторів розглядаються відносно різних базисів);
2) рух відображає пряму на пряму, а паралельні прямі переводить у паралельні, причому відстані між парами цих паралельних прямих рівні;
3) при русі відрізок переходить у рівний відрізок, а точка, яка ділить відрізок у деякому відношенні, переходить у точку, яка ділить образ відрізка у такому ж відношенні. Зокрема, при русі точка, яка є серединою відрізка переходить у точку, яка є серединою відрізка;
4) рух переводить півплощину у півплощину.
Крім перерахованих властивостей рухів вони, очевидно, володіють також деякими іншими властивостями, які не характерні для всієї групи афінних перетворень. Зокрема
5) при русі зберігається скалярний добуток векторів.
Дане твердження є наслідком властивості 1), а також того, що рух переводить ортонормований репер в ортонормований. Тому
6) при русі кути переходять у рівні кути, зокрема перпендикулярні прямі переходять у перпендикулярні.
Назвемо дві фігури 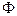 та
та  конгруентними, якщо в групі рухів знайдеться перетворення, яке фігуру
конгруентними, якщо в групі рухів знайдеться перетворення, яке фігуру 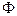 переводить у фігуру
переводить у фігуру  .
.
Відношення конгруентності є рефлексивним, симетричним та транзитивним. Справді,
1) кожна фігура переводиться в себе тотожнім перетворенням;
2) якщо фігура 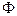 конгруентна фігурі
конгруентна фігурі  , то фігура
, то фігура  конгруентна фігурі
конгруентна фігурі 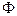 , оскільки вона переводиться в неї оберненим перетворенням;
, оскільки вона переводиться в неї оберненим перетворенням;
3) якщо фігура 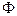 конгруентна фігурі
конгруентна фігурі  , а фігура
, а фігура  – фігурі
– фігурі  , то фігура
, то фігура 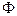 конгруентна фігурі
конгруентна фігурі  , оскільки вона переводиться в неї рухом, який є композицією двох рухів, перший з яких переводить
, оскільки вона переводиться в неї рухом, який є композицією двох рухів, перший з яких переводить 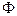 у
у  , а другий –
, а другий –  у
у  .
.
Відомо, що відношення, яке володіє властивостями рефлексивності, симетричності та транзитивності є відношенням еквівалентності. Відношенням еквівалентності, задане на деякій множині, розбиває цю множину на класи еквівалентності.
Відношення конгруентності, яке, в силу зроблених вище зауважень, є відношенням еквівалентності, розбиває множину всіх геометричних фігур на класи конгруентних фігур.
Дві фігури, які належать одному класу конгруентності, називають рівними.
Наприклад, клас конгруентних трикутників (або чотирикутників) утворюють всі трикутники (чотирикутники), у яких рівні відповідні сторони та кути. Всі кола однакового радіуса конгруентні. Нагадаємо, що у шкільному курсі геометрії доводиться ряд теорем, які визначають клас конгруентних трикутників. Це так звані ознаки рівностітрикутників. Відповідно до цих теорем, для рівності двох трикутників достатньо, щоб вони мали:
1) по три рівні сторони,
2) по дві рівні сторони та рівні кути між ними,
3) по рівній стороні та по два рівні прилеглі до них кути.
Дата публикования: 2015-09-17; Прочитано: 1875 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
