Властивості гомотетій

Розглянемо деякі властивості гомотетії. Як було сказано вище, гомотетія, будучи частинним випадком афінних перетворень, володіє всіма властивостями цих перетворень. Зокрема при гомотетії:

1) колінеарні вектори відображаються у колінеарні;

2) пряма відображається на пряму, причому паралельні прямі переходять у паралельні прямі;

3) відрізок переходить у відрізок, а точка, яка ділить відрізок у деякому відношенні, переходить у точку, яка ділить образ відрізка у такому ж відношенні. Зокрема середина відрізка переходить у середину відрізка;

4) півплощина переводиться у півплощину;

5) перетворення гомотетії можна задавати відповідністю двох реперів 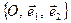та , де , .

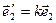Властивість 2) дозволяє запропонувати спосіб відшукання образу довільної точки, якщо відомий центр гомотетії та пара відповідних гомотетичних точок. Справді, нехай і задана довільна точка . Якщо ця точка не належить прямій , то образ точки буде знаходитися на перетині прямої та прямої, яка проходить через точку 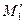паралельно до прямої (рис. 2). Якщо ж точка належить прямій , то спочатку знаходять образ довільної точки, яка не належить прямій , а потім за допомогою пари одержаних гомотетичних точок знаходять образ точки .

6). Нехай задані дві різні паралельні прямі та , причому довжини відрізків . Тоді існує єдина гомотетія, яка точку переводить у точку 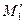, а точку – у точку . Такою є гомотетія з коефіцієнтом та з центром у точці, в якій перетинаються прямі та . Умова того, що задані паралельні прямі – різні, не є обов’язковою. Пропонуємо у вигляді окремої задачі побудувати точку, яка є центром гомотетії, у випадку, коли прямі та співпадають. Наведені міркування обґрунтовують той факт, що гомотетію можна задавати також двома парами відповідних точок, які задовольняють наведені вище обмеження.

Зупинимося на деяких інших властивостях, характерних для гомотетій.

Теорема 1. При гомотетії відстані між точками змінюються в одне і те ж число разів. Рівні відрізки відображаються на рівні відрізки.

Доведення. Нехай та . Тоді виконуються рівності та . Тому

.

Отже,

,

що доводить першу частину теореми. Оскільки довжини відрізків, які є образами рівних відрізків, відрізняються від довжин прообразів однаковим множником , то вони рівні.

Теорема доведена.

Теорема 2. При гомотетії зберігаються величини кутів.

Доведення цього факту є наслідком того, що при гомотетії паралельні прямі переводяться у паралельні.

Наслідок. Перпендикулярні прямі при гомотетії переходять у перпендикулярні.

Теорема 3. При гомотетії коло з радіусом переходить у коло з радіусом , центр якого знаходиться у точці, яка є образом центра заданого кола.

Доведення. Відмовляючись від чисто геометричного доведення, використаємо методи аналітичної геометрії. Помістимо початок прямокутної декартової системи координат у центрі гомотетії та нехай вісь проходить через центр заданого кола. Оскільки рівняння заданого кола можна записати у виді , то використавши формули гомотетії

,

отримаємо рівняння гомотетичної фігури у виді . Перетворивши одержане співвідношення до виду , бачимо, що воно визначає коло з радіусом , центр якого розташований у точці , яка є гомотетичною до центра заданого кола.

Теорема 4. Існує дві гомотетії, кожна із яких переводить деяке коло у довільне неконгруентне коло.

Доведення. Нехай задані два кола та з різними центрами у точках та і радіусами та , причому . Виберемо на колі точку та проведемо у колі діаметр, який паралельний прямій . Цей діаметр перетне коло у деяких точках та . Дві гомотетії, кожна з яких визначається двома парами відповідних точок та або згідно з властивістю 6) є шуканими і відображають коло на (рис. 3), оскільки відображають центр кола у центр кола , а точку на колі – у точку на колі . Центр однієї із гомотетій розташований у точці перетину прямих та , а її коефіцієнт при умові, що точки та розташовані по одну сторону відносно прямої , дорівнює . Центр другої гомотетії розташований у точці перетину прямих та , а її коефіцієнт рівний . Третьої гомотетії, яка відображає коло на нема, оскільки вона перевела б радіус у паралельний радіус кола , тобто у радіус або і співпала б із однією із двох побудованих гомотетій.

Якщо центри кіл співпадають, то коло на відображають дві гомотетії з центром у центрі даних кіл та коефіцієнтами і .