 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Частинні випадки рухів
|
|
Розглянемо частинні випадки співвідношень (2), тобто окремі види рухів.
1. При  та
та  формули (2) набувають вигляду
формули (2) набувають вигляду
 . (3)
. (3)
У цьому випадку точка  переводиться у точку
переводиться у точку  , тому
, тому  . Оскільки вектор
. Оскільки вектор  сталий і не залежить від вибору точки
сталий і не залежить від вибору точки  , то перетворення, яке задається формулами (3), є паралельним перенесенням на вектор
, то перетворення, яке задається формулами (3), є паралельним перенесенням на вектор  (рис. 3). Тобто задання
(рис. 3). Тобто задання  паралельного перенесення
паралельного перенесення  рівносильне заданню співвідношень (3). Послідовне виконання двох паралельних перенесень спочатку на вектор
рівносильне заданню співвідношень (3). Послідовне виконання двох паралельних перенесень спочатку на вектор  , а потім на вектор
, а потім на вектор  буде паралельним перенесенням на вектор
буде паралельним перенесенням на вектор  .
.
Воно задаватиметься співвідношеннями
 . (4)
. (4)
Оберненим до  є паралельне перенесення на вектор
є паралельне перенесення на вектор  . Воно задається рівностями
. Воно задається рівностями
 . (5)
. (5)
Співвідношення (4) та (5) аналітично обґрунтовують той факт, що множина паралельних перенесень утворює групу. Вона є підгрупою рухів, тому володіє всіма властивостями групи рухів. Оскільки додавання векторів комутативне, тобто для довільних векторів  та
та  виконується рівність
виконується рівність 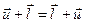 , то група паралельних перенесень є комутативною.
, то група паралельних перенесень є комутативною.
2. Нехай  ,
,  та
та  . Тоді рівності (2) запишуться у виді
. Тоді рівності (2) запишуться у виді
 . (6)
. (6)
Точки  та
та 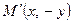 розташовані симетрично відносно осі
розташовані симетрично відносно осі  . Тому формули (6) задають осьову симетрію з віссю симетрії
. Тому формули (6) задають осьову симетрію з віссю симетрії  . Із перетворенням симетрії відносно прямої
. Із перетворенням симетрії відносно прямої  ми вже зустрічалися (лекція 26) та домовилися позначати його символом
ми вже зустрічалися (лекція 26) та домовилися позначати його символом  .
.
Оскільки осьова симетрія є рухом, то для неї теж виконуються всі властивості групи рухів. Очевидно, що осьова симетрія є рухом другого роду і змінює орієнтацію площини. Множина осьових симетрій з різними осями симетрії групи не утворює, оскільки композиція двох осьових симетрій не змінює орієнтації площини і тому не може бути осьовою симетрією.
 Покажемо, як можна шукати формули симетрії у випадку, коли віссю симетрії є довільна пряма.
Покажемо, як можна шукати формули симетрії у випадку, коли віссю симетрії є довільна пряма.
Нехай деяка пряма  , яка задана рівнянням
, яка задана рівнянням  , є віссю симетрії (рис. 4). Якщо точки
, є віссю симетрії (рис. 4). Якщо точки  та
та  розташовані симетрично відносно прямої
розташовані симетрично відносно прямої  , то координати середини відрізка
, то координати середини відрізка 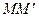 , тобто числа
, тобто числа  та
та  задовольнятимуть рівняння прямої. Тому виконується рівність
задовольнятимуть рівняння прямої. Тому виконується рівність
 .
.
З іншого боку, оскільки вектор  , який паралельний до прямої
, який паралельний до прямої  , є перпендикулярним до вектора
, є перпендикулярним до вектора  , то виконується рівність
, то виконується рівність  або
або
 .
.
Система, складена із двох одержаних рівнянь дозволяє виразити змінні  та
та  через
через  та
та  , тобто знайти шукані формули симетрії.
, тобто знайти шукані формули симетрії.
3. Нехай  та
та  . Тоді рівності (2) запишуться у виді
. Тоді рівності (2) запишуться у виді
 . (7)
. (7)
У даному випадку початок координат не змінює свого положення, а вектори

можна отримати поворотом початкового базису  навколо початку координат на кут
навколо початку координат на кут  . Таким чином, точку
. Таким чином, точку  ми отримуємо, виконавши поворот точки
ми отримуємо, виконавши поворот точки  навколо початку координат на кут
навколо початку координат на кут  (рис. 5). Співвідношення (7) називають формулами повороту. Нагадаємо, що поворот навколо деякої точки
(рис. 5). Співвідношення (7) називають формулами повороту. Нагадаємо, що поворот навколо деякої точки  на кут
на кут  ми позначаємо символом
ми позначаємо символом  .
.

При повороті на кут  формули (7) набувають виду
формули (7) набувають виду
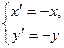
та виражають собою центральну симетрію з центром у початку координат, тобто  .
.
4. Нехай  та
та  . Тоді рівності (2) запишуться у вигляді
. Тоді рівності (2) запишуться у вигляді
 . (8)
. (8)
Перетворення, яке задається за допомогою одержаних співвідношень, називається ковзною симетрією.
Рівності
 ,
, 
дають підставу стверджувати, що ковзна симетрія являє собою композицію осьової симетрії з віссю симетрії  та паралельного перенесення на вектор
та паралельного перенесення на вектор  , який паралельний до осі симетрії.
, який паралельний до осі симетрії.
Позначають ковзну симетрію символом  , де
, де  – пряма, яка є віссю симетрії, а вектор
– пряма, яка є віссю симетрії, а вектор  паралельний до прямої
паралельний до прямої  (рис. 6). Для ковзної симетрії виконується рівність
(рис. 6). Для ковзної симетрії виконується рівність
 .
.

 4. Представлення рухів у вигляді композиції осьових симетрій.
4. Представлення рухів у вигляді композиції осьових симетрій.
Нехай деяке переміщення задане відповідністю двох ортонормованих реперів  та
та  . При осьовій симетрії відносно серединного перпендикуляра
. При осьовій симетрії відносно серединного перпендикуляра  до відрізка
до відрізка  точка
точка  перейде у точку
перейде у точку  , а вектори
, а вектори  та
та  – у вектори
– у вектори  та
та  . Нехай вектори
. Нехай вектори  та
та  утворюють кут
утворюють кут  , а пряма
, а пряма  є бісектрисою цього кута. Симетрія відносно прямої
є бісектрисою цього кута. Симетрія відносно прямої  сумістить вектор
сумістить вектор  з вектором
з вектором  . При цьому вектор
. При цьому вектор  або суміститься з вектором
або суміститься з вектором  , якщо базиси
, якщо базиси  та
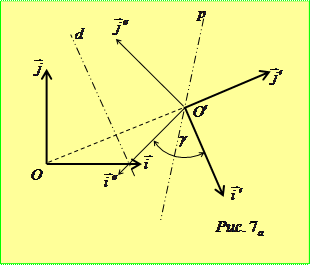
та  однаково орієнтовані (рис. 7а), або буде до нього протилежним у випадку протилежної орієнтації базисів (на рис. 7б – це вектор
однаково орієнтовані (рис. 7а), або буде до нього протилежним у випадку протилежної орієнтації базисів (на рис. 7б – це вектор  ). У першому випадку репер
). У першому випадку репер  перейде у репер
перейде у репер  за допомогою двох осьових симетрій, а у другому репери сумістяться після ще одної осьової симетрії – симетрії відносно прямої, яка проходить через точку
за допомогою двох осьових симетрій, а у другому репери сумістяться після ще одної осьової симетрії – симетрії відносно прямої, яка проходить через точку  паралельно до вектора
паралельно до вектора  .
.
Таким чином, доведено наступне твердження.
Теорема. Будь-який рух першого роду можна представити у вигляді композиції не більше, як двох осьових симетрій. Будь-який рух другого роду можна представити у вигляді композиції не більше, як трьох осьових симетрій.

Дата публикования: 2015-09-17; Прочитано: 1253 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
