 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Приклади задач
|
|
Розглянемо деякі задачі, при розв’язанні яких використовуються перетворення подібності.
 Задача 1. Довести, що точка
Задача 1. Довести, що точка 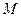 , яка є центром трикутника (точкою перетину медіан), точка
, яка є центром трикутника (точкою перетину медіан), точка 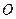 , яка є центром описаного навколо трикутника кола та ортоцентр
, яка є центром описаного навколо трикутника кола та ортоцентр  (точка перетину висот трикутника) лежать на одній прямій (так званій прямій Ейлера). При цьому виконується рівність
(точка перетину висот трикутника) лежать на одній прямій (так званій прямій Ейлера). При цьому виконується рівність  .
.
Доведення. Нехай у трикутнику  медіани
медіани  та
та  перетинаються у точці
перетинаються у точці 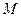 , висоти
, висоти 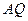 та
та  – у точці
– у точці  , а серединні перпендикуляри до сторін
, а серединні перпендикуляри до сторін  та
та  – у точці
– у точці 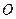 (рис. 4). Розглянемо гомотетію
(рис. 4). Розглянемо гомотетію  . Згідно із властивістю медіан трикутника
. Згідно із властивістю медіан трикутника  ,
,  . Таким чином, пряма
. Таким чином, пряма  при даній гомотетії відобразиться на паралельну пряму
при даній гомотетії відобразиться на паралельну пряму  , а пряма
, а пряма 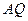 – на паралельну пряму
– на паралельну пряму  . Тому точка
. Тому точка  , у якій перетинаються прямі
, у якій перетинаються прямі  та
та 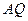 , перейде у точку перетину прямих
, перейде у точку перетину прямих  та
та  , тобто у точку
, тобто у точку 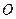 . Отже,
. Отже,  , або
, або  . Одержана рівність означає, що точки
. Одержана рівність означає, що точки 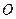 ,
, 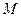 та
та  лежать на одній прямій, а також те, що виконується рівність
лежать на одній прямій, а також те, що виконується рівність  .
.
Задача 2. Довести, що середини основ трапеції, точка перетину її діагоналей та точка, в якій перетинаються прямі, яким належать бічні сторони трапеції, лежать на одній прямій.
 Доведення. Нехай задана трапеція
Доведення. Нехай задана трапеція  , діагоналі
, діагоналі  та
та  якої перетинаються у точці
якої перетинаються у точці  , точки
, точки 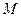 та
та 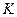 – середини онов відповідно
– середини онов відповідно  та
та  , а продовження бічних сторін перетинаються у точці
, а продовження бічних сторін перетинаються у точці 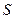 (рис. 5).
(рис. 5).
Розглянемо гомотетію  , де
, де  . Вона відображає точки
. Вона відображає точки  та
та  відповідно у точки
відповідно у точки  та
та  . Тому відрізок
. Тому відрізок  при цій гомотетії відображається на відрізок
при цій гомотетії відображається на відрізок  , а середина відрізка
, а середина відрізка  – точка
– точка 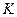 переходить у середину відрізка
переходить у середину відрізка  – точку
– точку 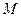 . Отже, точки
. Отже, точки 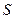 ,
, 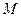 та
та 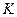 лежать на одній прямій. Гомотетія
лежать на одній прямій. Гомотетія  , де
, де  відображає точки
відображає точки  та
та  відповідно у точки
відповідно у точки  та
та  , відрізок
, відрізок  – на відрізок
– на відрізок  та переводить середину відрізка
та переводить середину відрізка  у середину відрізка
у середину відрізка  . Отже, точки
. Отже, точки  ,
, 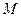 та
та 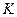 лежать на одній прямій. Таким чином, усі чотири точки, задані в умові задачі, належать одній прямій.
лежать на одній прямій. Таким чином, усі чотири точки, задані в умові задачі, належать одній прямій.
Зауважимо, що розглянута задача фактично дає відповідь на те, як за допомогою однієї двохсторонньої лінійки (тобто лінійки з двома паралельними краями) побудувати середину заданого відрізка. Побудова виглядає наступним чином. Нехай задано деякий відрізок  . За допомогою лінійки проводимо дві паралельні прямі, одна з яких містить заданий відрізок та поза одержаною смужкою вибираємо довільну точку
. За допомогою лінійки проводимо дві паралельні прямі, одна з яких містить заданий відрізок та поза одержаною смужкою вибираємо довільну точку 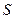 . Проводимо прямі
. Проводимо прямі  та
та  і знаходимо точки їх перетину з другою прямою (нехай це точки
і знаходимо точки їх перетину з другою прямою (нехай це точки  та
та  відповідно). Через точку
відповідно). Через точку 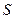 та точку перетину прямих
та точку перетину прямих  та
та  проводимо ще одну пряму. Точка
проводимо ще одну пряму. Точка 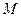 , у якій вона перетне відрізок
, у якій вона перетне відрізок  , є його серединою.
, є його серединою.
Задача 3. У даний трикутник вписати квадрат.
Розв’язання. Нехай  – заданий трикутник та
– заданий трикутник та  – квадрат, вершини
– квадрат, вершини  та
та  якого належать стороні
якого належать стороні  , а вершина
, а вершина  – стороні
– стороні  заданого трикутника. Нехай промінь
заданого трикутника. Нехай промінь  перетинає сторону
перетинає сторону  у точці
у точці  . Розглянемо гомотетію з центром у точці
. Розглянемо гомотетію з центром у точці  та коефіцієнтом
та коефіцієнтом  , яка точку
, яка точку 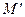 переводить у точку
переводить у точку 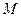 . Точки
. Точки  при вибраній гомотетії відобразяться у точки
при вибраній гомотетії відобразяться у точки  , які належать сторонам трикутника (рис. 6), причому
, які належать сторонам трикутника (рис. 6), причому  ॥
॥  ,
,  ॥
॥  і
і  ॥
॥ 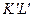 .
.


Чотирикутник  є шуканим квадратом, оскільки він є прямокутником з рівними сторонами (при гомотетії зберігається перпендикулярність прямих, а рівні відрізки переводяться у рівні відрізки).
є шуканим квадратом, оскільки він є прямокутником з рівними сторонами (при гомотетії зберігається перпендикулярність прямих, а рівні відрізки переводяться у рівні відрізки).
Після виконаного аналізу побудова шуканого квадрата є очевидною. Зауважимо, що задача має три розв’язки у випадку гострокутного трикутника, два розв’язки, якщо трикутник прямокутний та єдиний розв’язок, якщо трикутник тупокутний.
Задача 4. Побудувати трикутник за трьома висотами.
Розв’язання. Нехай  – висоти трикутника
– висоти трикутника  із сторонами
із сторонами  та
та 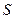 – його площа. Оскільки виконуються рівності
– його площа. Оскільки виконуються рівності  або
або  , то заданий трикутник подібний до трикутника із сторонами
, то заданий трикутник подібний до трикутника із сторонами  ,
,  ,
, 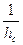 . Нехай
. Нехай  – висоти трикутника
– висоти трикутника  із сторонами
із сторонами  та
та  – його площа. З рівностей
– його площа. З рівностей  або
або  робимо висновок, що трикутник
робимо висновок, що трикутник  із сторонами
із сторонами  теж подібний до трикутника із сторонами
теж подібний до трикутника із сторонами  ,
,  ,
, 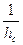 , тому трикутники
, тому трикутники  та
та  подібні.
подібні.
Таким чином, побудова трикутника за трьома висотами може виконуватися наступним чином:
1) будується трикутник  із сторонами
із сторонами  та у ньому проводяться висоти
та у ньому проводяться висоти  ;
;
2) будується трикутник  із сторонами
із сторонами  і у ньому проводиться одна із висот – нехай висота
і у ньому проводиться одна із висот – нехай висота  ;
;
3) виконується гомотетія  з центром у точці
з центром у точці 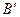 та коефіцієнтом
та коефіцієнтом  , яка переводить трикутник
, яка переводить трикутник  у шуканий трикутник
у шуканий трикутник  (рис. 7).
(рис. 7).
Задача має єдиний розв’язок, якщо можлива побудова трикутників  та
та  , тобто, якщо виконуються нерівності
, тобто, якщо виконуються нерівності 
 та
та  +
+  >
> 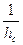 ,
,  +
+  >
>  ,
, 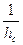 +
+  >
>  .
.

Дата публикования: 2015-09-17; Прочитано: 2739 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
