Поняття переміщення. Способи задання переміщень

Зупинимось на розгляді деяких частинних випадків афінних перетворень. Зокрема нас будуть цікавити ті перетворення, які зберігають відстані між точками.

Означення. Перетворення, при яких зберігаються відстані між точками, називаються переміщеннями (рухами або ізометричними перетвореннями).

Згідно із означенням, якщо точки та рухом переводяться у точки та , то для будь-яких точок та .

Насамперед покажемо, що переміщення є афінним перетворенням та встановимо, які умови потрібно накласти на коефіцієнти у формулах

, (1)

щоб дане афінне перетворення було переміщенням.

Як нам відомо, співвідношення (1) при умові , задають афінне перетворення, при якому точка та вектори і є образами елементів початкового репера .

Виберемо на площині довільний ортонормований репер , який перетворенням (1) переводиться у новий репер . Нехай , , , , а точки є відповідно образами точок при перетворенні (1). Оскільки при русі зберігаються відстані, то , . Відрізок , довжина якого дорівнює , переводиться у рівний відрізок , тому трикутник - прямокутний. Отже, вектори та утворюють ортонормований базис. Таким чином, при русі ортонормований репер переходить в ортонормований репер (тут ми використали традиційні для одиничних базисних векторів позначення: та ).

Нехай вектор утворює із вектором кут . Тоді

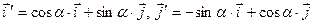
у випадку, коли базиси та орієнтовані однаково (рис. 1), та

у випадку протилежної орієнтації базисів (рис. 2).

Отже, якщо формули (1) задають переміщення, то

,

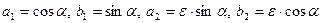де у випадку, коли базиси та орієнтовані однаково та у протилежному випадку.

Іншими словами, афінне перетворення, яке є рухом, визначається рівностями

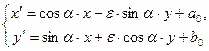. (2)

Навпаки, нехай деяке перетворення площини задане рівностями (2). Для двох точок та їх образів дістаємо

,

тобто таке перетворення є рухом.

Оскільки існує єдине афінне перетворення, яке один репер переводить в інший (лекція 26, п.1), то існує єдиний рух, який деякий ортонормований репер переводить в інший ортонормований репер.

Таким чином ми встановили, що переміщення однозначно можна задавати відповідністю двох ортонормованих реперів, або співвідношеннями

,

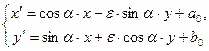де у випадку однойменної орієнтації базисів та і у випадку різнойменної орієнтації. В обох випадках визначник матриці перетворення

.

Зауважимо, що, поклавши у співвідношеннях (2) , можна досліджувати існування інваріантних (тобто таких, які переводяться в себе) точок переміщень.

Нам відомо, що існує єдине афінне перетворення , яке трикутник переводить у трикутник 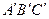(властивість 6, л. 26). Нехай – рух. Тоді трикутник перейде у рівний йому трикутник (трикутники рівні за трьома сторонами, оскільки зберігає довжини відрізків). Із єдиності випливає, що перетворення, яке є рухом, можна задавати також відповідністю двох рівних трикутників.