Інваріанти рівняння лінії

Розглянемо загальне рівняння лінії другого порядку

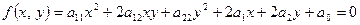. (1)

Для його перетворення застосуємо формули переходу до нової системи координат :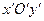

, , (2)

Ці співвідношення зв’язують координати точки у двох системах координат при паралельному перенесенні початкової системи в новий початок 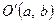з наступним її поворотом на кут 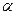(див. п. 3 – 4 лекції 21). У результаті рівняння (1) запишеться у вигляді

. (3)

При цьому квадратична форма, яка визначається групою старших членів рівняння (1)

перейде у квадратичну форму

.

Оскільки при паралельному перенесенні старші коефіцієнти у рівнянні не змінюються, то вважатимемо, що виконується тільки поворот системи. Тоді пучок квадратичних форм

,

який залежить від параметра , перейде в пучок

.

Справді, вираз перейде у рівний йому вираз , оскільки обидва вони дорівнюють квадрату відстані від точки до початку координат (при повороті відстань між точками не змінюється). Квадратична форма визначається матрицею

,

а квадратична форма – матрицею

.

В курсі лінійної алгебри доводиться той факт, що для матриць та квадратичної форми, яка розглядається у різних базисах, виконується рівність , де – матриця переходу від одного базису до іншого.

Оскільки при повороті системи координат на кут базисні вектори та зв’язані рівностями

,

то матриця переходу запишеться у вигляді

.

Очевидно, що 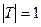. Тому .

Рівність

запишемо у розгорнутому виді

.

Одержана тотожність виконується для довільного , тому з неї випливають співвідношення

, .

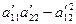Числа та , величина яких не залежить від вибору системи координат, очевидно, є шуканими інваріантами.

Для відшукання ще одного інваріанту в рівняннях (1) та (3) за допомогою співвідношень 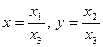, , перейдемо до однорідних координат. Рівняння лінії будуть

,

.

Оскільки ліві частини одержаних рівнянь тепер являють собою квадратичні форми, які визначаються матрицями

та

відповідно, то можна скористатися наведеними вище міркуваннями. Для цього запишемо формули (2) через однорідні координати у вигляді

,

,

.

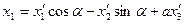Матриця переходу в даному випадку запишеться у виді

,

а її визначник, очевидно, рівний 1. Використавши рівність , дістаємо, що число

теж є інваріантом заданого рівняння.

Таким чином, числ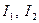а та 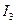є інваріантами рівняння лінії, тобто не змінюються при перетворенні рівняння (1) за допомогою формул (2).