Поняття ексцентриситету

Число називають ексцентриситетом еліпса та гіперболи. Нагадаємо, що число дорівнює відстані між фокусами, а – велика піввісь еліпса або дійсна піввісь гіперболи. Для еліпса , тому його ексцентриситет менший 1. Для гіперболи , отже, . Ексцентриситет параболи за означенням приймають рівним 1. Обґрунтуванням цього означення є так звана директоріальна властивість еліпса та гіперболи, яку буде розглянута у наступному пункті. Дослідимо, як залежить від зміни ексцентриситету форма лінії.

Для еліпса , тому . Якщо , то і довжини півосей вирівнюються. Форма еліпса при цьому наближається до кола.

Якщо , то , тобто еліпс стискається до осі .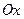

Для рівняння гіперболи виконується рівність , тому

.

Якщо , то , тобто асимптоти утворюють з віссю 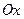все менший кут: гіпербола стискається до осі 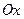. Якщо , то . У цьому випадку кут між асимптотами прямує до розгорнутого, а гіпербола стає все більш “витягнутою” вздовж осі .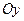

5. Поняття директрис. Директоріальна властивість ліній другого порядку.

Директрисою параболи ми називали пряму, задану рівнянням . Директрисами еліпса та гіперболи, які задані рівняннями (1) та (2), називають прямі .

Для еліпса 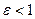, тому , а для гіперболи , тому 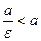, отже, директриси не перетинають ці лінії.

Будемо називати директрису d відповідною фокусу F, якщо вони лежать в одній півплощині відносно осі .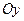

Теорема. Відношення відстаней від довільної точки еліпса (гіперболи) до фокуса та відповідної директриси є стала величина, рівна ексцентриситету.

Доведення. Доведемо теорему у випадку еліпса (для гіперболи доведення аналогічне). Враховуючи симетричність еліпса, розглянемо випадок правого фокуса F ₁(c;0) та відповідної директриси , рівняння якої (рис. 6). Нехай – довільна точка еліпса . Тоді, враховуючи вирази для фокальних радіусів, маємо

MF ₁= .

Обчислимо відстань від точки М до директриси d:

.

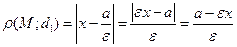При розкритті модуля враховано, що та , звідки . Отже, . Теорема доведена.

Для параболи (враховуючи означення) відстані від її довільної точки до фокуса та до директриси рівні, тому їх відношення дорівнює 1. Це обґрунтовує той факт, що ексцентриситет параболи приймають рівним 1.

Властивість, яку виражає доведена теорема, називають директоріальною властивістю ліній другого порядку (еліпса, гіперболи, параболи).