Найпростіші властивості гіперболи та її зображення

Дослідимо деякі властивості гіперболи. Її канонічне рівняння було одержано у виді

, (3)

де – модуль різниці відстаней від довільної точки гіперболи до фокусів та , .

Очевидно, що для розв’язків рівняння (2) виконується умова . Це означає, що точки гіперболи розташовані в півплощинах, які задаються нерівностями та . Аналогічно, як для еліпса, встановлюємо, що гіпербола симетрична відносно початку координат та координатних осей.

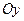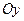Гіпербола перетинає тільки одну із координатних осей, а саме вісь у двох точках: та . Ці точки називають вершинами гіперболи, а відрізок – її дійсною віссю. Вісь гіпербола не перетинає, оскільки рівняння не має розв’язків. Відрізок , де точки та розташовані на осі на відстані від осі , називають уявною віссю. Число 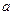називають дійсною, а число – уявною піввіссю гіперболи. Центр симетрії гіперболи (точку 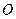) називають центром гіперболи.

Дослідимо форму та побудуємо графік гіперболи. Для цього, враховуючи симетричність лінії, розглядатимемо тільки першу координатну чверть, де, як легко одержати із (3), рівняння гіперболи має вигляд . Оскільки

, ,

то при 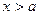, . Отже, графік гіперболи зростає при , починаючи від точки А ₁ та опуклий вверх.

Розглянемо, як у першій чверті точки гіперболи розташовані відносно прямої . Для цього через довільну точку проведемо вертикальну пряму до перетину з прямою в деякій точці та обчислимо різницю ординат точок N та M (рис. 3). Дістаємо

Оскільки різниця додатна, то точки прямої розташовані вище від точок гіперболи. При нескінченному зростанні абсциси х точки М дана різниця прямує до 0, тому точки гіперболи необмежено наближаються до прямої.

Якщо точки деякої лінії необмежено наближаються до певної прямої, рухаючись у нескінченність, то цю пряму називають асимптотою лінії.

Таким чином, прямі будуть асимптотами гіперболи.

Виконані дослідження дозволяють зобразити гіперболу (рис. 4).

Гіпербола, півосі якої рівні (), називається рівносторонньою. Її канонічне рівняння має вигляд

.

У новій системі координат, осі якої співпадають із асимптотами, які у даному випадку є перпендикулярними, рівносторонню гіперболу можна задати рівнянням

.

Її графік буде графіком функції оберненої пропорційності.

Більш детально питання про те, як змінюється рівняння лінії при переході до нової системи координат, буде розглянуто в лекції 21.

Параметричні рівняння гіперболи можна задати у вигляді рівностей

, , ,

де 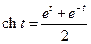(гіперболічний косинус), 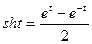(гіперболічний синус). Можливі також інші варіанти параметричного задання гіперболи, наприклад,

, , .

Для побудови точок гіперболи можна скористатися наступним прийомом. Будуємо коло довільного радіуса з центром у точці та коло з центром у точці 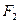, радіус якого на більший за радіус попереднього кола. Очевидно, що точки перетину побудованих кіл будуть належати гіперболі, оскільки відстані від них до центрів кіл відрізняються на .