Означення гіперболи та її канонічне рівняння. Вирази для фокальних радіусів

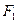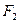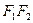
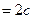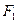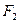Нехай на площині задані точки та та . Знайдемо геометричне місце точок площини, модуль різниці відстаней від кожної з яких до точок та є сталою величиною, що дорівнює заданому числу 2 а.

Будемо вважати, що 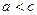. Якщо 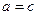, то шукане геометричне місце точок утворювало б два промені, які доповнюють відрізок F ₁ F ₂ до прямої. Якщо 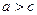, то шукана множина точок буде порожньою, що випливає з нерівності трикутника. Очевидно також, що a >0. При а =0 ми розглядали б точки, рівновіддалені від точок F ₁ та F ₂, тобто серединний перпендикуляр до відрізка F ₁ F ₂.

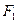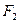Означення 2. Множина всіх точок площини, модуль різниці відстаней від кожної з яких до двох фіксованих точок та є сталою. Величиною, меншою від довжини відрізка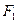 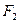, називається гіперболою.

Точки F ₁ та F ₂ називаються фокусами гіперболи. Для виведення рівняння гіперболи виберемо прямокутну декартову систему координат 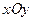так, як показано на рисунку 1, та припустимо, що 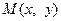– одна із точок шуканої множини. Згідно з означенням

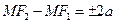. (7)

Оскільки 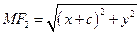та 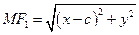, то з рівності (7) дістаємо

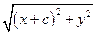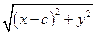
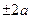= , (8)

звідки, звільнившись від радикала в лівій частині та звівши подібні доданки, одержуємо

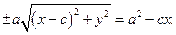(9)

Підносячи ще раз обидві частини рівності до квадрату, після очевидних спрощень дістанемо

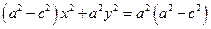. (10)

Оскільки 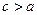, то 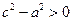, тому, ввівши позначення 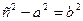, із останньої рівності отримуємо

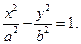(11)

Покажемо, що кожен розв’язок 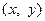одержаного рівняння задає точку 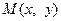на гіперболі, тобто, що для кожного розв’язку рівняння (11) виконується умова (7). Справді, із (11) дістаємо 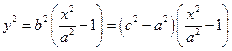, тому

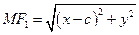
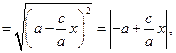
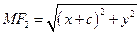
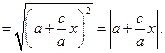
Із рівняння (11) випливає, що 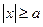. Оскільки 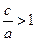, то для додатних х маємо 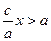, тому

, .

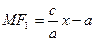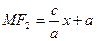Для 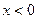дістаємо 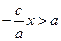, тому

, .

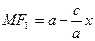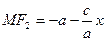В обох випадках виконується рівність (7), тому рівняння (11) є рівнянням гіперболи. Його називають канонічним рівнянням гіперболи. Відрізки 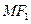та 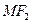називають фокальними радіусами точки М.