Означення еліпса. Канонічне рівняння. Вирази для фокальних радіусів

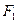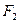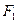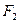Розглянемо на площині дві точки та , відстань між якими позначимо 2 с та поставимо задачу відшукання геометричного місця всіх точок, сума відстаней від кожної з яких до точок та є сталою, яка дорівнює деякому числу 2 а. Будемо вважати, що 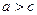, оскільки при 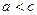шукана множина точок буде порожньою, а при 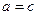утворить відрізок .

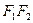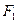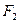Означення 1. Множина всіх точок площини, сума відстаней від кожної з яких до двох фіксованих точок та є сталою величиною, що більша від довжини відрізка 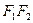, називається еліпсом.

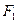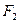Точки та називаються фокусам 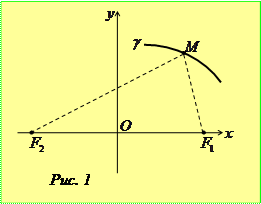и еліпса. Щоб скласти рівняння еліпса, введемо прямокутну декартову систему координат 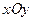, вибравши за точку 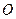середину відрізка 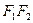та спрямувавши вісь 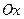вздовж прямої 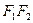(рис.1). Фокуси еліпса відносно введеної системи координат матимуть координати F ₁(c;0), F ₂(- c;0). Нехай M (x; y) – одна із точок шуканого геометричного місця 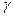. Тоді, згідно з означенням еліпса,

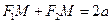. (2)

Скориставшись формулою відстані між двома точками, дістаємо

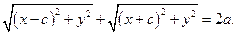
Для спрощення одержаного співвідношення, запишемо його у вигляді

,

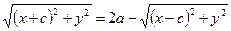звідки

,

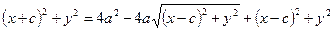або

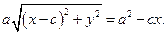(3)

Підносячи до квадрату обидві частини одержаної рівності, отримуємо

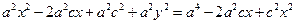(4)

або

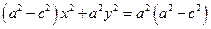. (5)

Оскільки a > c, то вираз 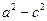додатний. Тому, ввівши заміну 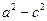= 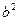та розділивши рівність (5) на 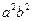, дістаємо

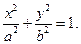(6)

Отже, координати кожної точки на еліпсі задовольняють рівняння (6). Покажемо, що кожен розв’язок рівняння (6) задає точку на еліпсі. Нехай 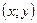– розв’язок рівняння (6) та М (x; y) – відповідна точка. Тоді пара чисел (x; y) задовольняє рівняння (5) та (4). Запишемо рівняння (4) у вигляді 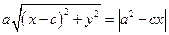, звідки випливає, що

.

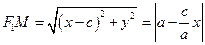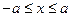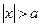Очевидно, що для розв’язків рівняння (6) повинна виконуватись умова (якщо , то 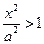і рівність (6) неможлива). Оскільки 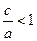, то 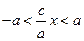, тому вираз 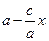– додатний. Таким чином,

. (7)

Міркуючи аналогічно, дістаємо

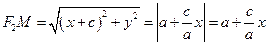. (8)

Тому 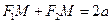, тобто точка М належить еліпсу. Таким чином, доведено, що рівняння (6) є рівнянням еліпса. Його називають канонічним рівнянням еліпса.

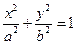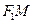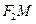Рівняння є рівнянням другого степеня, тому еліпс – це лінія другого порядку. Відрізки та називають фокальними радіусами точки М. Співвідношення (7), (8) дозволяють обчислювати довжини фокальних радіусів, знаючи тільки абсцису точки, яка належить еліпсу.