 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Взаємне розташування двох прямих у просторі
|
|
Як відомо, дві прямі в просторі можуть бути паралельними (зокрема співпадати), перетинатися або бути мимобіжними. Встановимо, як розпізнавати ці випадки, якщо кожна з прямих 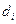 задана точкою
задана точкою 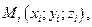 що належить прямій, та напрямним вектором
що належить прямій, та напрямним вектором 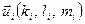
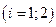 .
.
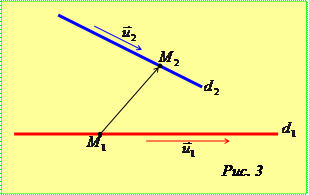 Очевидно, що випадок, коли обидві прямі лежать в одній площині (тобто паралельні або перетинаються), чи мимобіжні, залежить від того компланарні, чи ні вектори
Очевидно, що випадок, коли обидві прямі лежать в одній площині (тобто паралельні або перетинаються), чи мимобіжні, залежить від того компланарні, чи ні вектори 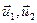 та
та 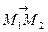 (рис. 3). Нагадаємо, що необхідною та достатньою умовою компланарності трьох векторів є рівність нулю їхнього мішаного добутку. Тому розглянемо число
(рис. 3). Нагадаємо, що необхідною та достатньою умовою компланарності трьох векторів є рівність нулю їхнього мішаного добутку. Тому розглянемо число
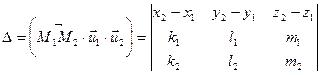 .
.
Якщо 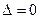 , то вектори
, то вектори 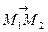 ,
, 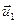 та
та 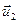 компланарні, тому прямі
компланарні, тому прямі 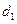 та
та  лежать в одній площині. Якщо при цьому вектори
лежать в одній площині. Якщо при цьому вектори 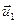 та
та 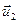 колінеарні, тобто виконуються умови
колінеарні, тобто виконуються умови
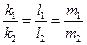 , (2)
, (2)
То.
Якщо 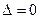 , а умова (2) не виконується, то прямі
, а умова (2) не виконується, то прямі 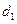 та
та 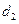 перетинаються. Прямі
перетинаються. Прямі 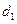 та
та 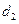 можуть співпадати, якщо крім умови (2) виконується також рівність
можуть співпадати, якщо крім умови (2) виконується також рівність
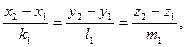
яка означає, що точка 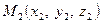 на другій прямій одночасно належить також і першій прямій.
на другій прямій одночасно належить також і першій прямій.
Якщо 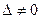 , то вектори
, то вектори 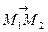 ,
, 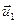 та
та 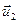 не компланарні, і прямі
не компланарні, і прямі 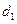 та
та 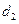 мимобіжні.
мимобіжні.
Кутом між двома мимобіжними прямими в просторі називають кут між двома прямими, що проходять через деяку спільну точку і паралельні до заданих прямих. У випадку аналітичного задання мимобіжних прямих 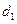 та
та 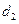 кут
кут 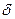 між ними шукають як кут між їхніми напрямними векторами
між ними шукають як кут між їхніми напрямними векторами 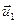 та
та 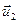
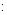
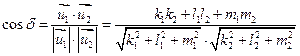 .
.
Дата публикования: 2015-09-17; Прочитано: 2072 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
