Поняття загального рівняння другого порядку

Розглянувши геометричні образи рівнянь першого степеня на площині та в просторі (пряма та площина), зупинимось на дослідженні рівнянь другого порядку.

Загальне рівняння другого порядку відносно змінних та можна записати у вигляді

, (1)

де хоча б один із коефіцієнтів a, b та c відмінний від нуля. З окремими випадками таких рівнянь ми уже зустрічалися, розглядаючи рівняння (коло з центром у точці , радіус якого дорівнює 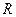), 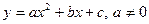(парабола, вісь якої паралельна до осі 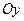), (або 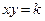, рівностороння гіпербола, дві вітки якої розташовані в першій та третій або другій та четвертій координатних четвертях у залежності від знаку параметра ). Проте наведені приклади не вичерпують усі можливі випадки ліній, які задаються рівнянням (1). Наприклад, рівняння визначає дві прямі, які перетинаються. У цьому легко переконатися, перетворивши рівняння до виду 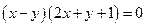. Рівняння має єдиний розв’язок , що стає очевидним, якщо його записати у вигляді . Рівняння або взагалі не задовольняє жодна пара дійсних чисел.

Скільки та які типи ліній визначає рівняння (1), ми дослідимо дещо пізніше, а поки що розглянемо деякі лінії, рівняння яких можна отримати, як частинні випадки рівняння (1).