Задачі. Задача 1. Знайти точку, симетричну до точки відносно площини , заданої рівнянням

Задача 1. Знайти точку, симетричну до точки відносно площини 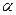, заданої рівнянням .

Розв’язання. Складемо параметричні рівняння прямої , яка перпендикулярна до площини 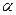Для цього використаємо точку та вектор , який, будучи перпендикулярним до площини 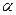, буде паралельним до прямої (рис. 5). Дістаємо

.

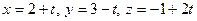Розв’язуючи систему рівнянь

,

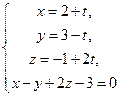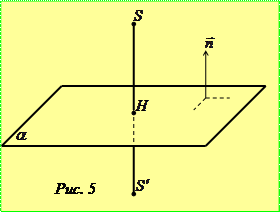знаходимо , Знайдена точка є точкою перетину прямої із заданою площиною. Нехай – точка, симетрична точці відносно площини 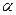. Тоді точка буде серединою відрізка . Із рівностей

дістаємо .

Відповідь. .

Задача 2. На якій відстані від початку координат проходить пряма :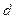

?

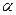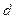Розв’язання. Проведемо через точку площину перпендикулярно до заданої прямої та знайдемо точку перетину прямої із 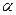. Очевидно, що вектор , який паралельний до прямої 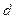, буде перпендикулярним до 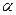, тому рівняння 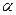запишеться у вигляді Тепер запишемо параметричні рівняння 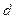та розв’яжемо систему рівнянь

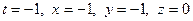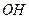Дістаємо . Отже, . Довжина відрізка є шуканою відстанню.

Відповідь. .

Задача 3. Знайти відстань між діагоналлю куба та мимобіжною діагоналлю однієї із його граней, якщо ребро куба дорівнює 1. Встановити, які саме точки діагоналей знаходяться на цій відстані.

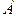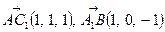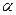Розв’язання. Нехай – заданий куб. Знайдемо відстань між мимобіжними прямими та . Для цього введемо у розгляд прямокутну декартову систему координат, вибравши за початок координат точку та спрямувавши осі та відповідно у напрямку ребер та (рис. 6). Знаходимо координати необхідних точок: та векторів: . Через діагональ проведемо площину , яка паралельна до прямої . Її рівняння запишеться у вигляді

або . Знаходимо відстань від точки 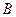до площини 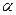: . Це і є шукана відстань. Щоб дати відповідь на питання, які з точок діагоналей знаходяться на знайденій відстані, складемо рівняння спільного перпендикуляра до прямих та . Для цього складемо рівняння площин 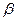та 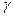, кожна з яких перпендикулярна до площини 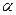та проходить через прямі та відповідно. Дістаємо

: , : ,

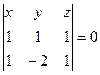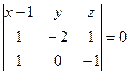звідки

, .

Таким чином, рівняння спільного перпендикуляра до прямих та запишеться у вигляді системи

.

Для всіх точок прямої , тому вона перетинає спільний перпендикуляр у точці .

Для кожної точки діагоналі виконується рівність . При цій умові спільному перпендикуляру належить точка . Легко перевірити, що точки та розташовані на відстані .