 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Задачі. Задача 1. Зобразити лінію перетину площин та
|
|
Задача 1. Зобразити лінію перетину площин  та
та  .
.
Розв’язання. Зобразимо площину  . Для цього знайдемо точки
. Для цього знайдемо точки  та
та  її перетину з осями
її перетину з осями 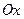 та
та 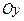 . Оскільки
. Оскільки  ||
|| 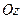 (в рівнянні площини відсутня змінна
(в рівнянні площини відсутня змінна  ), то, провівши через точки
), то, провівши через точки 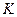 та
та  прямі
прямі  та
та 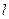 паралельно до осі
паралельно до осі 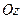 , дістанемо зображення площини
, дістанемо зображення площини  (рис. 6). На осі
(рис. 6). На осі 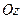 знаходимо точку
знаходимо точку  , яка належить площині
, яка належить площині  , і через неї проводимо прямі
, і через неї проводимо прямі  та
та  . Точка
. Точка 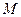 і прямі
і прямі 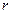 та
та  визначають площину
визначають площину  . Точка
. Точка  перетину прямих
перетину прямих 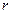 та
та  належить шуканій прямій перетину площин, оскільки обидві прямі лежать в одній площині (площині
належить шуканій прямій перетину площин, оскільки обидві прямі лежать в одній площині (площині 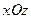 ) і перетинаються. Аналогічно, точка
) і перетинаються. Аналогічно, точка  перетину прямих
перетину прямих  та
та 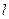 , які лежать в площині
, які лежать в площині 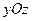 , теж належить лінії перетину. Таким чином, шуканою прямою є пряма
, теж належить лінії перетину. Таким чином, шуканою прямою є пряма  .
.

Задача 2. Скласти рівняння ортогональної проекції прямої 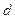 , заданої канонічним рівнянням
, заданої канонічним рівнянням  , на площину
, на площину  , задану рівнянням
, задану рівнянням  .
.
Розв’язання. Скористаємося вектором  який перпендикулярний до площини
який перпендикулярний до площини  та вектором
та вектором  , який паралельний до прямої
, який паралельний до прямої 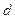 . Ці вектори не колінеарні, тому пряма
. Ці вектори не колінеарні, тому пряма 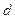 не перпендикулярна до
не перпендикулярна до  . Отже її проекцією буде деяка пряма
. Отже її проекцією буде деяка пряма  .
.
Другу площину  , якій належить s, проведемо через пряму
, якій належить s, проведемо через пряму 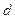 , перпендикулярно до
, перпендикулярно до  . Очевидно, що
. Очевидно, що  проходить через точку
проходить через точку  , яка належить прямій
, яка належить прямій 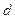 і паралельна до векторів
і паралельна до векторів  та
та 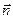 . Скориставшись співвідношенням (2), дістаємо рівняння площини
. Скориставшись співвідношенням (2), дістаємо рівняння площини  :
:
 ,
,
яке запишемо у вигляді
 ,
,
або

Рівняння шуканої проекції подамо у вигляді (10), як перетин площин  та
та  .
.
Відповідь. 
Задача 3. Три грані куба з ребром 1 належать координатним площинам. Побудувати переріз куба площиною
 .
.
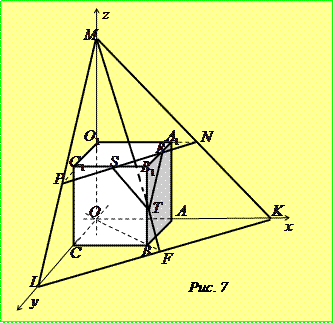 Розв’язання. Зобразимо заданий куб
Розв’язання. Зобразимо заданий куб 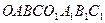 та площину
та площину  , побудувавши на осях точки
, побудувавши на осях точки  (рис. 7). Знаходимо точку
(рис. 7). Знаходимо точку  перетину прямих
перетину прямих 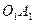 та
та 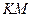 (обидві прямі лежать в площині
(обидві прямі лежать в площині 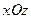 ) та точку P перетину прямих
) та точку P перетину прямих  та
та  . Пряма PN лежить у площині
. Пряма PN лежить у площині  та в площині
та в площині  і перетинає ребра верхньої грані куба в точках R та S. Тепер знаходимо точку
і перетинає ребра верхньої грані куба в точках R та S. Тепер знаходимо точку  перетину прямих
перетину прямих  та
та  і проводимо пряму
і проводимо пряму  , яка перетне ребро
, яка перетне ребро  у деякій точці T.
у деякій точці T.
Відповідь. Трикутник  .
.
Задача 4. Три ребра трикутної піраміди взаємно перпендикулярні, а їх довжини дорівнюють  та
та 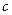 . Знайти ребро куба, вписаного в цю піраміду, якщо одна з вершин куба співпадає з вершиною піраміди
. Знайти ребро куба, вписаного в цю піраміду, якщо одна з вершин куба співпадає з вершиною піраміди
Розв’язання. Нехай ребра 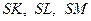 трикутної піраміди взаємно перпендикулярні. Впишемо в цю піраміду куб, одна з вершин якого (на рис. 8 – точка
трикутної піраміди взаємно перпендикулярні. Впишемо в цю піраміду куб, одна з вершин якого (на рис. 8 – точка  ) належить грані
) належить грані  піраміди. Нехай ребро куба дорівнює
піраміди. Нехай ребро куба дорівнює 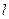 . Тоді у системі координат, зображеній на рисунку 8, рівняння площини
. Тоді у системі координат, зображеній на рисунку 8, рівняння площини  запишеться у вигляді
запишеться у вигляді 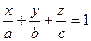 . Оскільки точка
. Оскільки точка  належить цій площині, то виконується рівність
належить цій площині, то виконується рівність 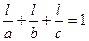 . З одержаного рівняння знаходимо
. З одержаного рівняння знаходимо  .
.
Відповідь.  .
.

Дата публикования: 2015-09-17; Прочитано: 1036 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
