Геометричний зміст знаку виразу

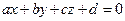Задамо в просторі афінну систему координат та розглянемо площину , задану рівнянням . Вона розбиває весь простір на два півпростори із спільною границею – площиною . Знайдемо умови, які визначають ці півпростори.

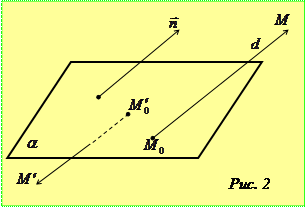Виберемо на даній площині деяку точку 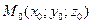та проведемо через неї паралельно до вектора 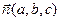пряму 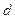(рис. 2). Даний вектор не може бути паралельним до площини , оскільки тоді, згідно з лемою про паралельність вектора та площини (лекція 7, п. 3), виконувалася б рівність 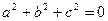, що неможливо. Нагадаємо, що у прямокутній системі координат вектор 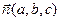перпендикулярний до площини .

Виберемо на прямій 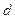довільну точку 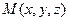та запишемо рівності 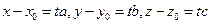, які випливають із колінеарності векторів 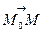та 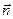, оскільки останні зв’язані між собою рівністю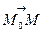 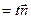. Обчислимо значення виразу 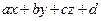у точці :

.

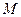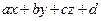
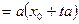
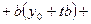
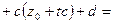
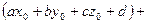
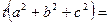
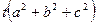Оскільки 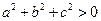, то знак виразу 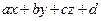залежить від знаку множника 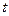. Зокрема при 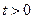вектори 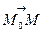та 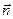напрямлені однаково, тому всі точки 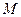, для яких 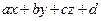>0, будуть утворювати півпростір, обмежений площиною (цьому півпростору належить кінець вектора 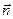). При 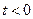вектори 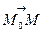та 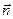напрямлені протилежно, а множина точок, для яких 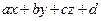<0, утворює інший півпростір, границею якого є площина .