Геометричні образи рівнянь першого степеня із трьома змінними

Лекція 9. Різні способи задання прямої та площини в просторі

План

Геометричні образи рівнянь першого степеня із трьома змінними.

Різні способи задання площини.

Загальне рівняння площини та його частинні випадки.

Різні способи задання прямої в просторі.

Задачі.

Геометричні образи рівнянь першого степеня із трьома змінними.

Рівняння з трьома змінними вигляду визначає в просторі деяку поверхню. Розглянемо випадок, коли це рівняння першого степеня відносно змінних 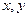та , тобто записується у вигляді

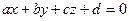. (1)

Тут 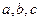– деякі числові коефіцієнти, які одночасно не дорівнюють нулю (тобто виконується умова 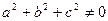), 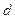– довільне число.

Покажемо, що це рівняння визначає в просторі деяку площину. Нехай у рівнянні (1) 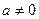та 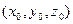– один із розв’язків цього рівняння. Введемо в розгляд два не колінеарні вектори 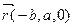та 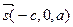та відкладемо їх від точки 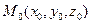. Нехай та 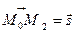. Тоді точки 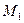та 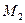матимуть наступні координати: .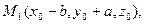

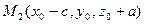Підставляючи координати точки 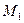у рівняння (1), дістаємо

_,

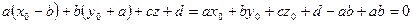тобто точка 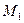належить поверхні. Аналогічні обчислення виконуються для точки 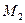. Отже, обидві точки належать поверхні (1).

Нехай 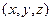– довільний розв’язок (1) а 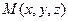– відповідна точка на поверхні. Обчисливши мішаний добуток векторів 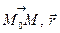та 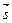, дістаємо

,

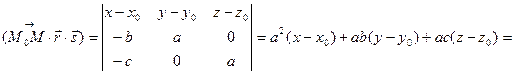
що доводить компланарність векторів. Тому точки 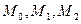та 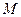лежать в одній площині.

Навпаки, для довільної точки 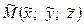, що належить побудованій площині, міркуючи аналогічно, отримуємо, що 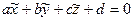, тобто координати цієї точки є розв’язком рівняння (1).

Отже, рівняння (1) визначає в просторі деяку площину.