Множення вектора на скаляр. Властивості

Нехай заданий деякий вектор 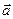та дійсне число .

Означення 8. Добутком вектора 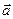на число називають такий вектор , який задовольняє наступні умови:

1) довжина цього вектора ,

2) , якщо та 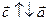, якщо .

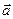При згідно з пунктом 1) означення , тому результатом множення довільного вектора на 0 є нульовий вектор . Добуток вектора на число записують у вигляді .

Множення вектора на число має ряд властивостей. Виділимо серед них наступні:

1) ;

2) ;

3) ;

4) ;

5) (асоціативність множення відносно числових множників та );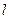

6) (дистрибутивність множення відносно числового множника);

7) (дистрибутивність множення відносно векторного множника).

Доведення властивостей 1) – 4) очевидне.

Для доведення властивості 5) доцільно розглянути випадки:

а) ; б) ; в) ; г) ; д) одне з чисел l i t або обидва ці числа дорівнюють нулю.

У випадку а), оскільки , то . Враховуючи те, що , дістаємо, що . Отже, . Очевидно, що , тобто вектори та однаково напрямлені. Рівність їхніх довжин випливає із рівності

.

Таким чином, згідно з означенням рівності векторів, властивість 5) у випадку а) доведена.

Випадки б), в) та г) розглядаються аналогічно.

У випадку д) рівність 5) виконується, оскільки обидві її частини є нульовими векторами.

Властивість 6) випливає із подібності трикутників та 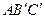(див. рис. 8 при та рис. 9 при ). При доведення властивості 6) очевидне.

Для доведення властивості 7) потрібно розглянути випадки, коли числа та l одного знаку (обидва додатні або від’ємні) або різних знаків.

Нехай та . Тоді і . Вектори та 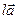протилежно напрямлені, а також .

Тому

.

Вектор має напрям вектора , тобто спів напрямлений з вектором 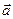. Отже, в обох частинах рівності 7) маємо однаково напрямлені вектори однакової довжини, тобто ці вектори рівні.

Аналогічно розглядається випадок та випадок, коли . Якщо одне із чисел t або l рівне нулю, або вони обидва дорівнюють нулю, то рівність 7) очевидна.

Зауважимо, що якщо , то вектор одиничний і однаково напрямлений із вектором 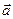. Справді, .

Якщо задані два ненульові вектори 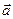та 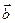, то вектори та матимуть однакові довжини . Тоді вектор + задає напрям бісектриси кута, утвореного векторами 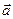та 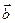, оскільки він матиме напрям діагоналі паралелограма, побудованого на векторах і , який є ромбом.