 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Понятие ранга
|
|
В 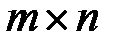 -матрице
-матрице  выберем
выберем  строк с номерами
строк с номерами  и столько же столбцов с номерами
и столько же столбцов с номерами  . Определитель матрицы из элементов, находящихся в этих строках и столбцах, обозначим
. Определитель матрицы из элементов, находящихся в этих строках и столбцах, обозначим  и назовем минором
и назовем минором  -го порядка матрицы
-го порядка матрицы  . Например, у матрицы
. Например, у матрицы  три минора 2-го порядка:
три минора 2-го порядка:
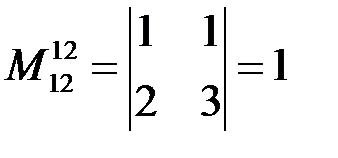 ,
,  и
и  .
.
Рангом (ненулевой) матрицы называется наибольший из порядков ненулевых миноров. Ранг матрицы  мы будем обозначать
мы будем обозначать  . Таким образом, равенство
. Таким образом, равенство  означает, что у матрицы
означает, что у матрицы  есть ненулевой минор порядка
есть ненулевой минор порядка  , а все миноры больших порядков, если они имеются, равны нулю (см. пример 4.2.1). Ранг характеризует степень «вырожденности» матрицы. Например, для квадратной матрицы
, а все миноры больших порядков, если они имеются, равны нулю (см. пример 4.2.1). Ранг характеризует степень «вырожденности» матрицы. Например, для квадратной матрицы  -го порядка крайние случаи: нулевая матрица
-го порядка крайние случаи: нулевая матрица  самая «вырожденная», у нее все миноры нулевые и естественно считать
самая «вырожденная», у нее все миноры нулевые и естественно считать  0; и невырожденная матрица
0; и невырожденная матрица  с
с  , ее ранг
, ее ранг  .
.
Так как миноров у матрицы даже небольших размеров много, то нахождение ранга по определению связано с громоздкими вычислениями. Для нахождения ранга можно применять элементарные преобразования матриц, аналогичные элементарным преобразованиям систем, описанным в п. 3.1.3:
а) перестановки любых двух строк местами;
б) прибавление к строке другой строки, умноженной на число;
в) удаление строки, состоящей из нулей;
г) те же действия, что и в пунктах а)–в), для столбцов.
При этих преобразованиях ненулевые миноры переходят в ненулевые и потому они не меняют ранга. После преобразований получим матрицу вида
 ,
,
у которой минор

и потому ранг равен 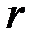 (см. пример 4.2.2).
(см. пример 4.2.2).
Матрицы  и
и  называются эквивалентными (обозначение
называются эквивалентными (обозначение  ), если у них одинаковый ранг:
), если у них одинаковый ранг:  .
.
Дата публикования: 2015-09-17; Прочитано: 353 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
