 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Понятие определителя
|
|
Для каждой квадратной матрицы 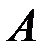
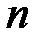 -го порядка (
-го порядка (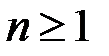 ) определено число, обозначаемое
) определено число, обозначаемое 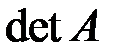 или
или 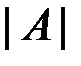 и называемое определителем матрицы
и называемое определителем матрицы 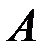 (определителем
(определителем 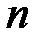 -го порядка).
-го порядка).
При 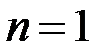 матрица
матрица 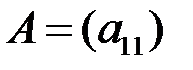 состоит из одного элемента,
состоит из одного элемента,
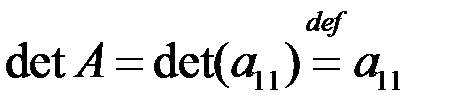 .
.
При 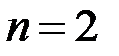
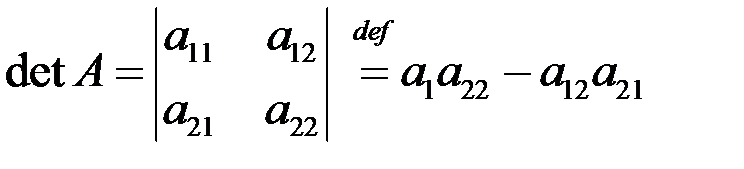 . (1.1)
. (1.1)
При любом 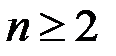
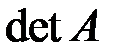 – сумма всевозможных произведений
– сумма всевозможных произведений 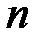 элементов матрицы
элементов матрицы 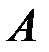 , стоящих в разных строках и разных столбцах, со знаком
, стоящих в разных строках и разных столбцах, со знаком 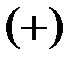 или
или 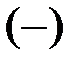 , определяемым порядком сомножителей:
, определяемым порядком сомножителей:
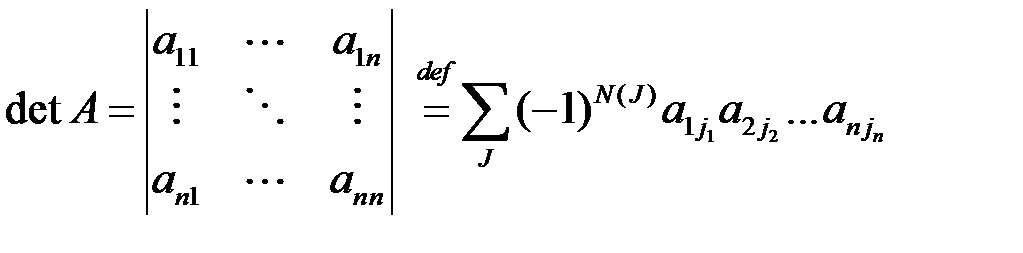 . (1.2)
. (1.2)
Здесь:
сомножители 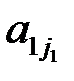 ,
, 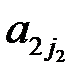 , …,
, …, 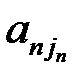 выбраны последовательно из 1-ой, 2-ой, …,
выбраны последовательно из 1-ой, 2-ой, …, 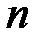 -ой строки;
-ой строки;
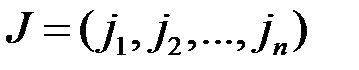 – соответствующая последовательность номеров столбцов;
– соответствующая последовательность номеров столбцов;
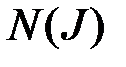 – число инверсий в последовательности
– число инверсий в последовательности  : число
: число 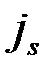 и число
и число 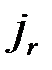 с большим номером
с большим номером 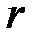 (
(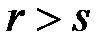 ) образуют инверсию, если
) образуют инверсию, если 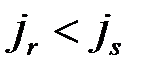 . При четных
. При четных 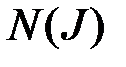 величина
величина 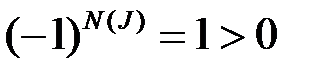 , при нечетных
, при нечетных 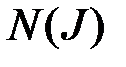 –
– 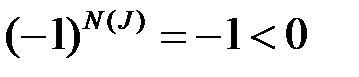 .
.
Формула (1.1), конечно, частный случай общей формулы (1.2) (см. пример 1.2.6).
При 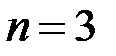 формула (1.2) принимает вид
формула (1.2) принимает вид
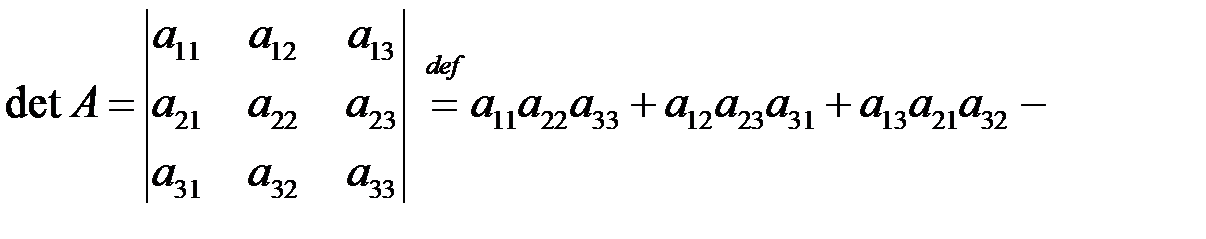
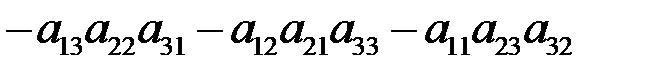 . (1.3)
. (1.3)
Из (1.2) следует, что определитель треугольной матрицы равен произведению элементов главной диагонали: 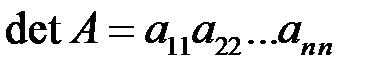 .
.
Дата публикования: 2015-09-17; Прочитано: 280 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
