Умножение матриц

Пусть – -матрица, – -матрица, то есть число столбцов у 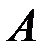равно числу строк у , или более наглядно:

длина строки 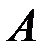матрицы высоте столбца матрицы .

Произведением матрицы 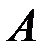на матрицу называется 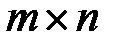-матрица, обозначаемая или , в -ой строке, -м столбце которой стоит элемент, равный сумме произведений элементов -ой строки на соответствующие элементы -го столбца:

(). (2.1)

Если длина строки матрицы 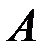не равна высоте столбца матрицы , то произведение не определено!

Для любых квадратных матриц 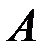и одного порядка их произведение определено и также является квадратной матрицей -го порядка.

Свойства умножения матриц: Для любых квадратных матриц 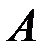, , одного порядка и любого числа

1) ;

2) и ;

3) , где – единичная матрица, элементы которой, стоящие на главной диагонали равны 1, а все остальные равны 0;

4) ,

5) .

Аналогичные 1)-4) свойства имеют место и для любых матриц при условии, что все выписанные произведения определены.

На умножение матриц (даже квадратных) уже не переносятся все свойства умножения чисел. В частности, нет перестановочности: в общем случае (пример 2.2.2); равенство , где – нулевая матрица возможно при и (задача 2.3.11).