 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема о среднем значении
|
|
Теорема 7. Если  и
и  для
для 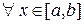 , то
, то  такое, что
такое, что
 . (15)
. (15)
 Положим
Положим
 ;
;
тогда равенство (15) очевидно. Включение  следует из оценок (14).
следует из оценок (14).
▲
Теореме 7 можно придать другую форму, если учесть включение  .
.
Теорема 8. Если  , то
, то  такое, что
такое, что
 . (16)
. (16)
 |
 Пусть
Пусть  ,
,  . Так как функция
. Так как функция  непрерывна на
непрерывна на  , то для
, то для  по теореме о промежуточных значениях непрерывной функции получаем, что
по теореме о промежуточных значениях непрерывной функции получаем, что  такое, что
такое, что  . Отсюда и из теоремы 7 получим равенство (16). ▲
. Отсюда и из теоремы 7 получим равенство (16). ▲
Рис. 2.
Теорема о среднем имеет простой геометрический смысл: существует точка  такая, что площадь криволинейной трапеции
такая, что площадь криволинейной трапеции  равна площади прямоугольника
равна площади прямоугольника  , имеющего высоту
, имеющего высоту  и основание
и основание  (рис. 2).
(рис. 2).
5. Интеграл с переменным верхним пределом. Сейчас перед нами стоит задача вывода основной формулы интегрального исчисления, которая устанавливает связь между понятиями определенного интеграла и первообразной.
До сих пор мы рассматривали определенный интеграл с постоянными пределами интегрирования  и
и  . Очевидно, что при изменении одного из пределов (например, верхнего) величина интеграла будет изменяться.
. Очевидно, что при изменении одного из пределов (например, верхнего) величина интеграла будет изменяться.
Рассмотрим этот вопрос подробнее. Если  , то
, то  интегрируема по любой части этого отрезка, и поэтому для
интегрируема по любой части этого отрезка, и поэтому для 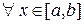 существует интеграл
существует интеграл
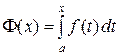 ,
,
называемый интегралом с переменным верхним пределом.
Значение функции  раскрывает следующая теорема.
раскрывает следующая теорема.
Теорема 9. Если  , то функция
, то функция 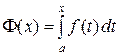 дифференцируема в любой внутренней точке
дифференцируема в любой внутренней точке  этого отрезка (
этого отрезка ( ), причем
), причем  .
.
 Зафиксируем любое значение
Зафиксируем любое значение  и придадим ему приращение
и придадим ему приращение  столь малое, чтобы точка
столь малое, чтобы точка  лежала внутри отрезка
лежала внутри отрезка  , т.е.
, т.е.  . Тогда
. Тогда  . Найдем производную функции
. Найдем производную функции  . Имеем
. Имеем
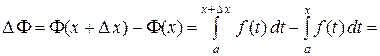
 .
.
Теперь к полученному интегралу применим теорему о среднем значении:
 ,
,
где  , если
, если  (или
(или  , если
, если  ). Отсюда
). Отсюда  . Так как функция
. Так как функция  непрерывна на
непрерывна на  и
и  при
при 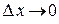 , то
, то
 .
.
Поэтому
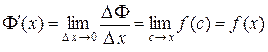 . ▲
. ▲
Замечание. Нами установлено, что любая непрерывная на отрезке  функция
функция  имеет на этом отрезке первообразную, а именно, функцию
имеет на этом отрезке первообразную, а именно, функцию 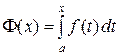 . Поскольку всякая другая первообразная для функции
. Поскольку всякая другая первообразная для функции  может отличаться от
может отличаться от  только на постоянную, то установлена связь между неопределенным и определенным интегралами в виде
только на постоянную, то установлена связь между неопределенным и определенным интегралами в виде
 ,
,
где  – произвольная постоянная.
– произвольная постоянная.
В силу вышеизложенных соображений теорему 9 часто называют теоремой о существовании первообразной для непрерывной функции.
6. Формула Ньютона-Лейбница. Теорема 9 не только указывает на связь между понятиями неопределенного и определенного интеграла, но и дает практический способ вычисления определенных интегралов в случае, когда подынтегральная функция непрерывна.
Теорема 10. Если функция  , то
, то
 , (17)
, (17)
где  – первообразная для функции
– первообразная для функции  . Формула (17) называется формулой Ньютона-Лейбница.
. Формула (17) называется формулой Ньютона-Лейбница.
 Поскольку функция
Поскольку функция  непрерывна на отрезке
непрерывна на отрезке  , то она интегрируема на нем и, значит, существует
, то она интегрируема на нем и, значит, существует  . Далее, в силу непрерывности функции
. Далее, в силу непрерывности функции  на
на  у нее на этом отрезке существует первообразная (теорема 9).
у нее на этом отрезке существует первообразная (теорема 9).
Мы установили, что функция 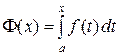 является одной из первообразных для функции
является одной из первообразных для функции  ; следовательно, для любой первообразной
; следовательно, для любой первообразной  имеем
имеем
 . (18)
. (18)
Отметим, что равенство (18) выполняется для 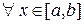 .
.
Поскольку  и из (18)
и из (18)  , то
, то  . Следовательно,
. Следовательно, 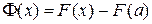 , в частности,
, в частности,  . Но
. Но 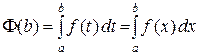 , откуда получаем равенство (17). ▲
, откуда получаем равенство (17). ▲
Разность  принято условно записывать в виде
принято условно записывать в виде  , поэтому формула (17) в краткой записи выглядит так:
, поэтому формула (17) в краткой записи выглядит так:
 .
.
7. Методы вычисления определенных интегралов. Так как формула Ньютона-Лейбница сводит задачу вычисления определенного интеграла от непрерывной функции к нахождению первообразной, то все основные методы вычисления неопределенных интегралов переносятся и на задачу вычисления определенных интегралов. Сформулируем эти методы с учетом специфики определенных интегралов.
Теорема 11 (о замене переменной). Пусть:
1)  ,
,  ;
;
2)  для
для  ;
;
3)  .
.
Тогда
 .
.
Для доказательства этого равенства достаточно применить к обеим его частям формулу Ньютона-Лейбница, учитывая при этом, что если  будет первообразной для
будет первообразной для  , то функция
, то функция  будет первообразной для
будет первообразной для  .
.
Пример. 
 .
.
Теорема 12 (об интегрировании по частям). Пусть  . Тогда
. Тогда
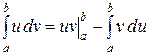 .
.
Справедливость этой формулы следует из равенства  и применения формулы Ньютона-Лейбница к интегралу от функции
и применения формулы Ньютона-Лейбница к интегралу от функции 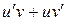 , для которой первообразной будет функция
, для которой первообразной будет функция  .
.
Пример. 
 .
.
Равенство (19) легко модифицировать для вычисления площадей плоских фигур самых различных конфигураций.
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Определенные интегралы имеют многочисленные приложения в самых разнообразных задачах. Здесь мы ограничимся рассмотрением некоторых геометрических приложений.
1. Вычисление площадей.
а) Площадь криволинейной трапеции
Площадь  криволинейной трапеции, ограниченной сверху графиком функции
криволинейной трапеции, ограниченной сверху графиком функции  , снизу – отрезком
, снизу – отрезком  оси
оси  , а по бокам – прямыми
, а по бокам – прямыми  и
и  , вычисляется по формуле
, вычисляется по формуле
 . (19)
. (19)
Обоснование этой формулы было дано ранее при введении понятия определенного интеграла. А именно, было показано, что интегральная сумма 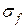 представляет собой приближенное значение площади криволинейной трапеции, и это приближенное значение тем точнее, чем «мельче» разбиение отрезка
представляет собой приближенное значение площади криволинейной трапеции, и это приближенное значение тем точнее, чем «мельче» разбиение отрезка  . Точное значение площади
. Точное значение площади  получается как предел интегральных сумм при
получается как предел интегральных сумм при  , если он, конечно, существует. Но указанный предел является ни чем иным как определенным интегралом
, если он, конечно, существует. Но указанный предел является ни чем иным как определенным интегралом  .
.
Равенство (19) легко модифицировать для вычисления площадей плоских фигур самых различных конфигураций.
Если верхняя граница криволинейной трапеции задана уравнениями в параметрической форме  ,
,  ,
,  , причем
, причем  ,
,  , то произведем в формуле (19) замену переменной, полагая
, то произведем в формуле (19) замену переменной, полагая  ,
,  . Тогда получим
. Тогда получим
 .
.
Пример. Вычислить площадь фигуры, ограниченной эллипсом 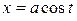 ,
,  (
( ).
).
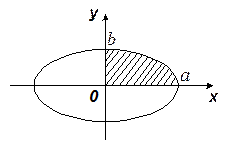 |
Рис. 3.
 Эллипс симметричен относительно осей координат, поэтому достаточно вычислить площадь части фигуры, находящейся в I четверти (рис. 3). Следовательно, искомая площадь равна
Эллипс симметричен относительно осей координат, поэтому достаточно вычислить площадь части фигуры, находящейся в I четверти (рис. 3). Следовательно, искомая площадь равна

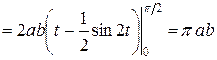 .
.
В частности, если полуоси эллипса равны ( ), то получаем известную формулу площади круга
), то получаем известную формулу площади круга  . ▲
. ▲
б) Площадь криволинейного сектора
Пусть кривая задана в полярных координатах уравнением  ,
,  , причем функция
, причем функция  непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке  . Плоскую фигуру, ограниченную дугой
. Плоскую фигуру, ограниченную дугой  этой кривой и двумя лучами, составляющими с полярной осью углы
этой кривой и двумя лучами, составляющими с полярной осью углы  и
и  (
(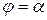 ,
,  ), называют криволинейным сектором (рис. 4).
), называют криволинейным сектором (рис. 4).
 |
Рис. 4.
Площадь криволинейного сектора
 . (20)
. (20)
 Разобьем произвольно отрезок
Разобьем произвольно отрезок  точками
точками  на
на  частей, выберем на каждом частичном отрезке
частей, выберем на каждом частичном отрезке  произвольно точку
произвольно точку  (
( ) и построим круговые секторы с радиусами
) и построим круговые секторы с радиусами  . В результате получим веерообразную фигуру, площадь которой приближенно равна площади
. В результате получим веерообразную фигуру, площадь которой приближенно равна площади  криволинейного сектора:
криволинейного сектора:
 ,
,
где  . С другой стороны, площадь веерообразной фигуры является интегральной суммой для интеграла (20). Так как функция
. С другой стороны, площадь веерообразной фигуры является интегральной суммой для интеграла (20). Так как функция  непрерывна на отрезке
непрерывна на отрезке  , то предел этой суммы при
, то предел этой суммы при  существует и равен интегралу (20). Следовательно, и площадь криволинейного сектора численно равна этому определенному интегралу:
существует и равен интегралу (20). Следовательно, и площадь криволинейного сектора численно равна этому определенному интегралу:
 . ▲
. ▲
Пример. Вычислить площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда:  , где
, где  – положительное число.
– положительное число.

 |
Рис. 5.
При изменении  от
от 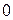 до
до 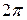 полярный радиус описывает кривую, ограничивающую криволинейный сектор
полярный радиус описывает кривую, ограничивающую криволинейный сектор  (рис. 5). Поэтому по формуле (20) имеем
(рис. 5). Поэтому по формуле (20) имеем
 . ▲
. ▲
Расстояние от точки  до полюса равно
до полюса равно 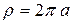 . Поэтому круг радиуса
. Поэтому круг радиуса  имеет площадь
имеет площадь  , т.е. площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда, равна
, т.е. площадь фигуры, ограниченной полярной осью и первым витком спирали Архимеда, равна  площади круга с радиусом, равным наибольшему из полярных радиусов витка. К этому выводу пришел еще Архимед.
площади круга с радиусом, равным наибольшему из полярных радиусов витка. К этому выводу пришел еще Архимед.
2. Длина дуги кривой. Пусть требуется определить длину дуги  кривой
кривой  ,
, 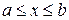 , где
, где 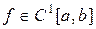 . Разобьем отрезок
. Разобьем отрезок  на
на  частей точками
частей точками  . Тогда длина
. Тогда длина 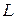 дуги
дуги  приближенно равна длине ломаной, вписанной в данную кривую:
приближенно равна длине ломаной, вписанной в данную кривую:
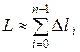 , (21)
, (21)
где  – длина хорды (одного звена ломаной)
– длина хорды (одного звена ломаной)  (рис. 6). Здесь точка
(рис. 6). Здесь точка  имеет координаты
имеет координаты  . Естественно длиной
. Естественно длиной 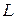 дуги
дуги  считать предел длин ломаных, вписанных в эту кривую, при
считать предел длин ломаных, вписанных в эту кривую, при  , где
, где 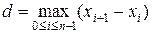 :
:
 , (22)
, (22)
 |
если, конечно, этот предел существует.
Рис. 6.
По теореме Пифагора имеем  . Но в силу теоремы Лагранжа получим
. Но в силу теоремы Лагранжа получим
 ,
,
где  . Тогда
. Тогда
 .
.
Если подставить эти равенства в правую часть соотношения (21), то получим интегральную сумму функции  на отрезке
на отрезке  . Функция
. Функция  непрерывна на отрезке
непрерывна на отрезке  , поэтому предел (22) этой суммы существует и равен определенному интегралу
, поэтому предел (22) этой суммы существует и равен определенному интегралу
 . (23)
. (23)
Пример. Вычислить длину полукубической параболы  , если
, если 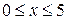 .
.
 Общее уравнение полукубической параболы имеет вид
Общее уравнение полукубической параболы имеет вид  (рис. 7). В данном случае нужно найти длину дуги верхней ветви. Из уравнения
(рис. 7). В данном случае нужно найти длину дуги верхней ветви. Из уравнения  находим:
находим:  . Следовательно, по формуле (23) получим
. Следовательно, по формуле (23) получим
 . ▲
. ▲
 |
Рис. 7.
 |
3. Объем тела вращения. Пусть функция
 непрерывна и неотрицательна на отрезке
непрерывна и неотрицательна на отрезке  . Найдем объем тела, образованного вращением криволинейной трапеции, ограниченной кривой
. Найдем объем тела, образованного вращением криволинейной трапеции, ограниченной кривой  и прямыми
и прямыми  ,
,  ,
,  , вокруг оси
, вокруг оси  (рис. 8).
(рис. 8).
Рис. 8.
Разобьем отрезок  на
на  частей точками
частей точками  . На каждом частичном отрезке
. На каждом частичном отрезке 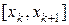 выберем произвольную точку
выберем произвольную точку  и построим прямоугольник высотой
и построим прямоугольник высотой  . При вращении вокруг оси
. При вращении вокруг оси  каждый прямоугольник опишет цилиндр радиуса
каждый прямоугольник опишет цилиндр радиуса  и высоты
и высоты  . Искомый объем
. Искомый объем  приближенно равен сумме объемов таких цилиндров (и это равенство тем точнее, чем «мельче» разбиение отрезка
приближенно равен сумме объемов таких цилиндров (и это равенство тем точнее, чем «мельче» разбиение отрезка  ):
):
 .
.
С другой стороны, правая часть равенства является интегральной суммой для функции  по отрезку
по отрезку  . Так как функция
. Так как функция  непрерывна на
непрерывна на  , то существует конечный предел этой суммы при
, то существует конечный предел этой суммы при  :
:
 .
.
 |
Пример. Вычислить объем тора. (Тором называется тело, получающееся при вращении круга радиуса
 вокруг оси, лежащей в его плоскости на расстоянии
вокруг оси, лежащей в его плоскости на расстоянии  от центра круга (
от центра круга ( ). Форму тора имеет, например, баранка.)
). Форму тора имеет, например, баранка.)
 Пусть круг вращается вокруг оси
Пусть круг вращается вокруг оси  (рис. 9).
(рис. 9).
Рис. 9.
Объем тора можно представить как разность объемов тел, полученных от вращения криволинейных трапеций  и
и  вокруг оси
вокруг оси  .
.
Уравнение окружности с центром в точке  и радиуса
и радиуса  имеет вид
имеет вид
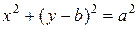 .
.
При этом уравнение верхней полуокружности 
 ,
,
а уравнение нижней полуокружности 
 .
.
Используя формулу для объема тела вращения, получаем для объема  тора выражение
тора выражение

 . ▲
. ▲
При выводе всех формул основное внимание надо обратить на метод решения: подсчитываемую величину разбиваем на части, каждую часть подсчитываем с некоторой погрешностью – получается интегральная сумма (в разобранных примерах – для непрерывной функции, и потому существуют соответствующие интегралы), а затем переходим к пределу, за счет чего получается точная формула.
НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ
Понятие определенного интеграла вводилось и изучалось, во-первых, в предположении, что интегрируемая функция должна быть ограниченной на отрезке интегрирования, во-вторых, сам отрезок должен быть конечным. Если хотя бы одно из этих необходимых требований не выполнено, то определенный интеграл не существует.
Оказывается, существуют классы функций, для которых, хотя и нарушены указанные требования, можно говорить о существовании определенного интеграла. Естественно, при этом определенный интеграл понимается не в обычном смысле, а рассматривается некоторое его обобщение. Укажем два основных класса таких функций.
1. Несобственные интегралы первого рода. Пусть 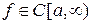 . Тогда
. Тогда  и, следовательно,
и, следовательно,  для
для  .
.
Определение. Несобственным интегралом 1-го рода функции  на промежутке
на промежутке  называют предел
называют предел
 .
.
Если этот предел существует и конечен, то несобственный интеграл называют сходящимся, в противном случае – расходящимся.
Пример. Рассмотрим несобственный интеграл 1-го рода функции  на промежутке
на промежутке  . При
. При  имеем:
имеем:
 .
.
Отсюда следует, что при  несобственный интеграл расходится, а при
несобственный интеграл расходится, а при  он сходится, причем
он сходится, причем
 ,
,  .
.
Легко убедиться, что рассматриваемый несобственный интеграл расходится и при  (проверьте!).
(проверьте!).
Несобственный интеграл вида  вводится аналогичным образом. Интеграл
вводится аналогичным образом. Интеграл 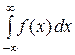 определяется с использованием свойства аддитивности определенного интеграла:
определяется с использованием свойства аддитивности определенного интеграла:
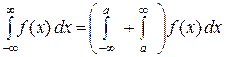 .
.
2. Несобственные интегралы второго рода. Пусть  , где
, где  и
и  – некоторые числа, причем
– некоторые числа, причем  при
при  (функция неограничена). Ясно, что тогда
(функция неограничена). Ясно, что тогда  .
.
Возьмем  . Тогда
. Тогда  и, следовательно,
и, следовательно,  .
.
Определение. Несобственным интегралом 2-го рода функции  на промежутке
на промежутке  называют предел
называют предел
 .
.
Если этот предел существует и конечен, то несобственный интеграл называют сходящимся, в противном случае – расходящимся.
Так же, как и выше, определяют интеграл от функции, неограниченной в окрестности точки  .
.
Пример. Исследовать на сходимость несобственный интеграл 2-го рода функции  ,
,  , на промежутке
, на промежутке  . При
. При  ,
,  имеем:
имеем:
 .
.
Из полученных соотношений следует, что если  , то несобственный интеграл расходится; если же
, то несобственный интеграл расходится; если же  , то сходится, причем
, то сходится, причем
 ,
,  .
.
Рассматриваемый несобственный интеграл расходится и при  (проверьте!).
(проверьте!).
Наконец, если  при
при  , где
, где  , то полагают
, то полагают
 .
.
Дата публикования: 2015-09-17; Прочитано: 970 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
