 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Свойства определенного интеграла
|
|
Сначала расширим понятие определенного интеграла. В определении мы считали, что  . Распространим определение на случаи
. Распространим определение на случаи  и
и  , полагая
, полагая
 и
и  .
.
1) Если 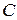 – константа, то
– константа, то  .
.
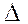 Интегральная сумма
Интегральная сумма  для функции
для функции  при любом разбиении отрезка
при любом разбиении отрезка 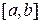 равна
равна
 ,
,
откуда  . ▲
. ▲
2) Если 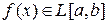 и
и  , то
, то  .
.
3) Если 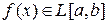 , то
, то  для любого отрезка
для любого отрезка  .
.
4) Аддитивность интеграла. Для любых чисел  имеет место равенство
имеет место равенство
 . (12)
. (12)
(Здесь предполагается, что интегралы, входящие в доказываемую формулу, существуют.)
 Допустим сначала, что
Допустим сначала, что  . Так как предел интегральной суммы
. Так как предел интегральной суммы  не зависит от способа разбиения отрезка
не зависит от способа разбиения отрезка 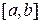 , то будем разбивать
, то будем разбивать 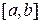 так, чтобы точка
так, чтобы точка  была точкой разбиения. Если, например,
была точкой разбиения. Если, например,  , то
, то  можно разбить на две суммы:
можно разбить на две суммы:
 ,
,
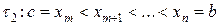 ,
,
 .
.
Переходя в этом равенстве к пределу при 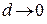 , получаем равенство (12).
, получаем равенство (12).
Суть доказанного свойства состоит в том, что определенный интеграл по всему отрезку равен сумме интегралов по его частям.
Доказательство для другого расположения точек 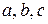 легко сводится к рассмотренному случаю. Пусть, например,
легко сводится к рассмотренному случаю. Пусть, например,  ; тогда по доказанному имеем:
; тогда по доказанному имеем:
 ,
,
откуда получаем
 ,
,
т.е. опять пришли к равенству (12). ▲
5) Линейность интеграла. Если  и
и  , то для любых
, то для любых 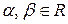 функция
функция  . При этом справедливо равенство
. При этом справедливо равенство
 . (13)
. (13)
В частности, из (13) получаем:
 (при
(при  ),
),
 (при
(при  ).
).
 Для произвольного разбиения отрезка
Для произвольного разбиения отрезка  имеем
имеем
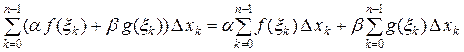 .
.
Переходя в равенстве к пределу при  , получим соотношение (13). ▲
, получим соотношение (13). ▲
6) Если  и
и  для
для 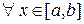 , то
, то
 .
.
(Подумайте о геометрическом истолковании этого свойства.)
 Рассмотрим функцию
Рассмотрим функцию  (см. свойство 5). Любая интегральная сумма
(см. свойство 5). Любая интегральная сумма  для функции
для функции  на
на  неотрицательна, т.к.
неотрицательна, т.к.  и
и 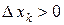 для
для  . Переходя к пределу при
. Переходя к пределу при  в неравенстве
в неравенстве  , получаем
, получаем
 ,
,
и осталось снова воспользоваться свойством 5. ▲
7) Если  и
и  для
для 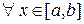 , то
, то
 . (14)
. (14)
 Следует из свойства 1 и свойства 6. ▲
Следует из свойства 1 и свойства 6. ▲
Дата публикования: 2015-09-17; Прочитано: 369 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
