Метод интегрирования по частям основан на равенстве

, (5)

называемом формулой интегрирования по частям, в котором и – две дифференцируемые на промежутке функции. Равенство (5) получается с помощью формулы дифференцирования произведения двух функций.

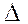Докажем (5). По правилу дифференцирования произведения получим

;

следовательно, 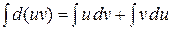. Учитывая второе из равенств (1), получим (5). ▲

Формула (5) позволяет свести задачу вычисления интеграла к вычислению интеграла , что в ряде случаев проще.

Примеры. 1) Вычислить . Положим , ; тогда , . Так как в качестве можно брать любую функцию вида , то возьмем . Отсюда и из формулы (5) получим

.

2) Вычислить . Положим , ; тогда , . Отсюда

.

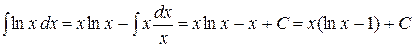Применяя формулу (5), следует разбить подынтегральное выражение на два множителя: и таким образом, чтобы вычислялся или хотя бы упрощался интеграл . Нельзя выбирать и произвольно, иначе можно получить еще более сложный интеграл. Метод интегрирования по частям позволяет вычислять, например, интегралы типа

(a) , , ;

(b) , , ;

(c) , ,

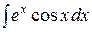а также подобные им. В случае (a) следует полагать ; в случае (b) – ; в случае (c) – . При этом для интегралов вида (a) и (b) требуется ровно 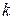раз применять формулу (5), а для интегралов вида (c) требуется двукратное применение формулы.

Пример. Применим метод интегрирования по частям для вычисления интеграла

. (6)

Полагая , , получим

.

Но

.

Поэтому

.

Отсюда

. (7)

Полученная формула сводит вычисление интеграла к вычислению интеграла с меньшим на единицу показателем степени. Формулы такого типа называют рекуррентными. Применим, например, формулу (7) к вычислению интеграла . Так как интеграл является табличным, а именно, , то из (7) получим (при ):

. ▲